GeoGebra

Description. Finding Geometric Medians and Geometric Centers on a circle from discrete sample points.

Autor:Roman Chijner
Applet https://www.geogebra.org/m/qpmtdkuw is used to study the distribution of geometric medians and centers on the circle of radius R, „induces“ by the discrete sample of movable points in the x-y plane. There is a set lP={p1, p2,...,pn} of points and {(xi,yi)∈ℝ²:i = 1,...,n} -their coordinates. Let a point (x,y) minimize a function of the sum of distances from this point to points lP. It is called Fermat's point https://en.wikipedia.org/wiki/Fermat_point or the Geometric median https://en.wikipedia.org/wiki/Geometric_median of the set lP. 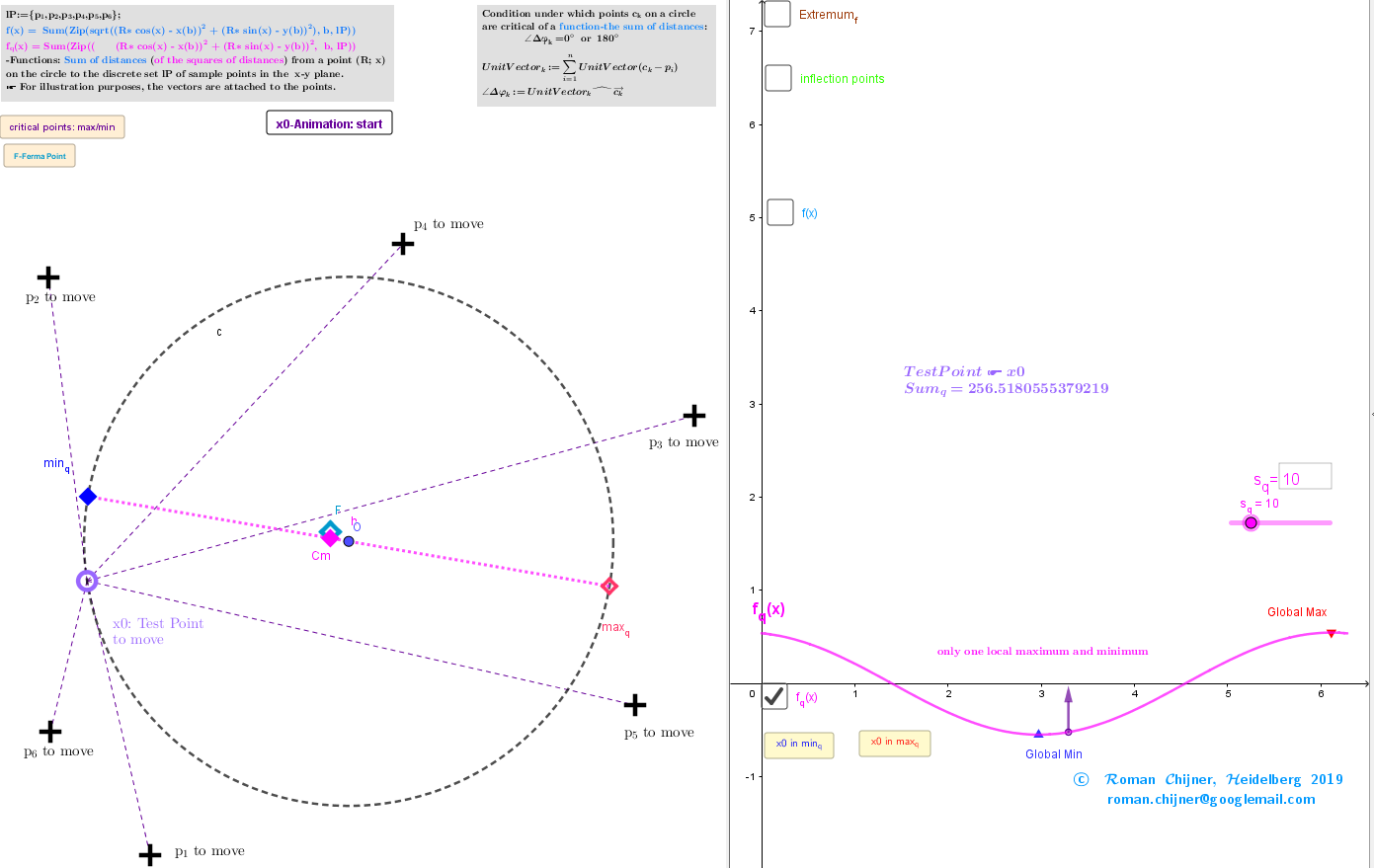The point Cm minimizes a function of the sum of squared distances and is called the center of mass https://en.wikipedia.org/wiki/Center_of_mass, centroid or Geometric Center https://en.wikipedia.org/wiki/Centroid of the set lP. Problem: find the positions of extreme points (and global minima and maxima too) of the function of sum (squares of the sum) of distances not on the entire x-y plane, but in its restricted region. Definitions of geometric medians and centers can be generalized, in the sense that the extreme points of the sum (squares of the sum) of distances function searched in a restricted region of a x-y plane.

Geometric Medians in restricted region(circle)

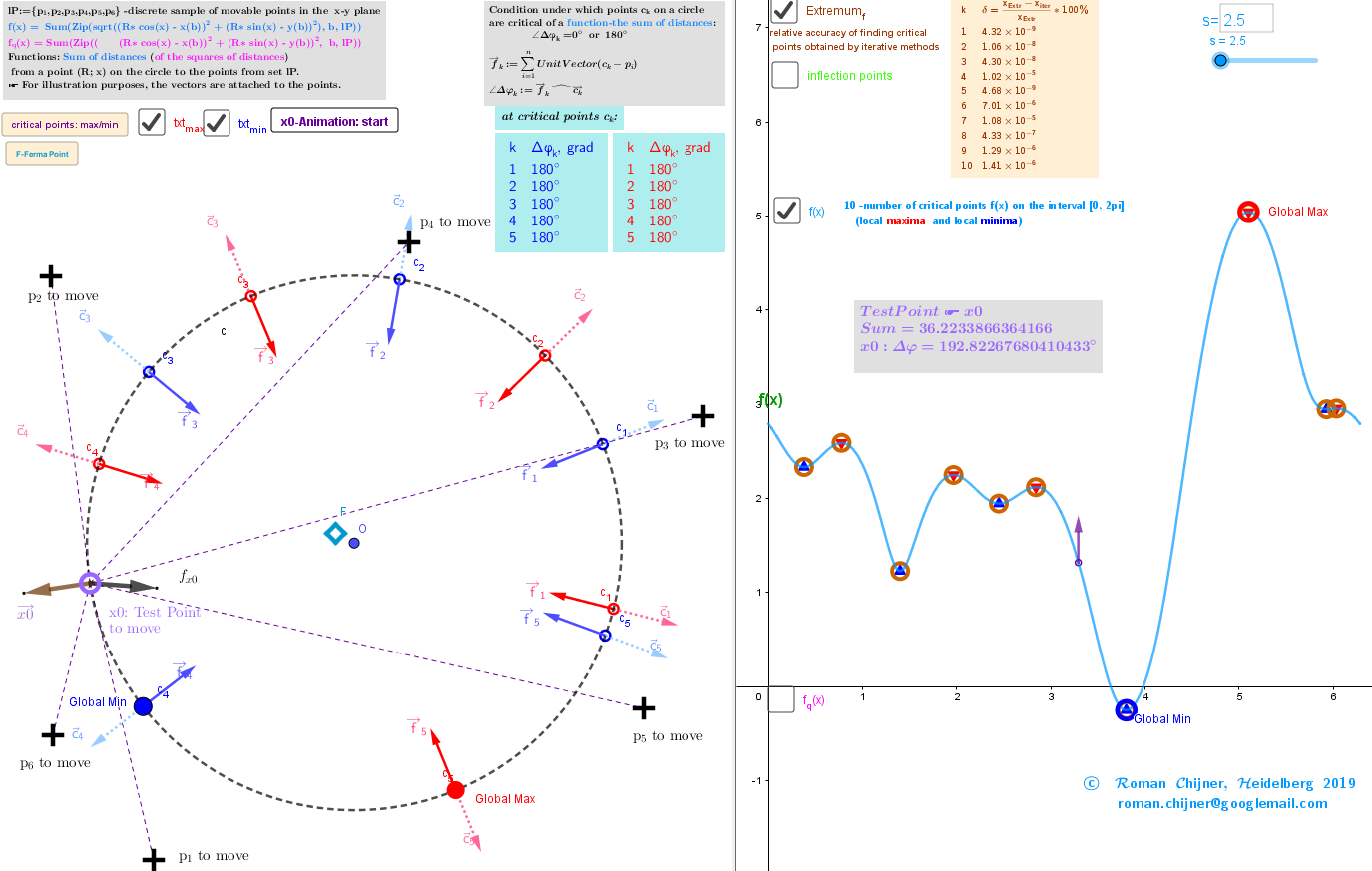
Geometric Medians in restricted region(circle)
The Geometric Median is defined here as point on circle from where the function of sum of the distances to each point pi's have at that point either the local minimum or local maximum or a stationary point of inflection. Critical points can be found using Lagrange multipliers as (Λ(x,y ,λ)=f(x,y )+λ*g(x,y )) finding the Extreme values of the function : f(x,y)= -sum of the distances from (x,y) to each point pi's, subject to a constraining equation: g(x,y)= - point (x,y)∈L. Let L be a circle of radius R around the point O: L:={∈ℝ²: ||||=R}. I.e. it is necessary to find the critical points f(x,y) subject to: g(x,y)=0. Further we will use positional vectors :=(x,y )T : f(x,y)=and g(x,y)=-R. The gradients are: :=∇f=and :=∇g =/R -gradient of the magnitude of a position vector r. There is a system of equations: ∇f(x,y)= λ*∇g(x,y). A local optimum occurs when ∇f(x,y) and ∇g(x,y) are parallel, and so ∇f is some multiple of ∇g. ☛ Thus, condition for a point c on a restricted region L to be GM is: the the resultant vector -sum of all unit vectors from the set of points lP to this point c is parallel to its positional vector , i.e. the angle Δφ between these two vectors is multiple of π .There are no explicit Geometric Medians formulas, in contrast to Geometric Centers explicit formulas. The solution of the system of equations can be found use iterative procedures.

Iterative formulas

I propose iterative procedures in which each step produces is a more accurate approximation: =R*UnitVector() finds the Maxima -c points and =R*UnitVector() finds the Minima -c points.

Geometric Centers in restricted region(circle)

Geometric Centers in restricted region(circle)
The Geometric Center is defined here as point on circle from where the sum of the squares of all Euclidean distances to each point pi's have at that point: local minimum, maximum or a stationary point of inflection. Critical points can be found using Lagrange multipliersas (Λ(x,y,λ)=f(x,y)+λ*g(x,y)) finding the Extreme values of the function : fq(x,y)= -sum of the squares of the distances to the points pi, subject to a constraining equation: g(x,y)=x2+y2-R2 - points (x,y)∈L. I.e. it is necessary to find the critical points f(x,y) subject to: g(x,y)=0. Let's denote the resulting point as Sum(lP):= , then ∇f/2=n*(x,y)- or ∇f/2=n*(x,y)-Sum(lP) and ∇g/2=(x,y): ⇒(x,y)∼Sum(lP). The point (x,y) that minimize the sum of the squares of the distances to the points pi is the Geometric Center (gravity center, barycenter, center of mass, centroid) GC: Cm= -its coordinates are the averages of the coordinates of the points from set lP. https://en.wikipedia.org/wiki/Center_of_mass . ☛ In this problem there are only two critical points (x,y)∈L. The Axis passing through the radius vector of the point Sum(lP) passes through the center of mass Cm and intersects the circle L at two points: one corresponds to the global maximum, the other- to the global minimum. Their coordinates have explicit formulas: GCmin= R* UnitVector(Sum(lP)) and GCmax= - R*UnitVector(Sum(lP)) - two antipodal points on circle. These points can be found using the Steiner theorem too. With applet you can visually observed and explore these solutions at different positions of the points from set lP. By changing the positions of points from lP, click on the "F-Ferma Point" and "critical points: max/min" buttons to find the new positions of geometric medians and centers in ℝ² and on the selected circle L. To evaluate the accuracy of the proposed iterative methods for finding critical points click on checkbox "Extremum_f". In polar coordinates functions f(x,y), fq (x,y) (in Cartesian coordinates x,y) are functions of one variable f(x), fq(x) depending only on the angular position (polar variable x) of the point on the circle of radius R. The dependencies of these functions on the angular position x of a point on a circle for a given location of points from lP are shown on the right side of the applet.
Applets in a book: Description. Finding Geometric Medians and Geometric Centers on a circle from discrete sample points. Applet. Finding Geometric Medians and Geometric Centers on a circle from discrete sample points. Method of Lagrange multipliers. Relative positioning of repulsive movable points on a circle. Generating an extreme arrangements of points on a circle Generating an extreme arrangements of points on a sphere Generating an extreme arrangements of points on a sphere with more structured calculation program-GeoGebra Forum- https://help.geogebra.org/topic/geogebra-windows-portable-zip-for-december

Nowe zasoby

Odkryj zasoby

Odkryj tematy