Tangente de un ángulo y sombra de un edificio
En su tránsito diario, el sol sale y se pone, y entre estos dos eventos alcanza su altura máxima en el horizonte. La sombra de los objetos sobre la superficie terrestre depende de la altura de éstos y de la posición del sol.
A medida que el sol sube desde el horizonte, las sombras de los objetos se van haciendo más pequeñas. ¿De qué depende el tamaño de la sombra de un objeto y cómo podría calcularse?
Como la altura del sol es dificil de calcular, es más sencillo tomar el ángulo que forma con el objeto que va a hacer sombra, de manera que se forma un triángulo rectángulo.
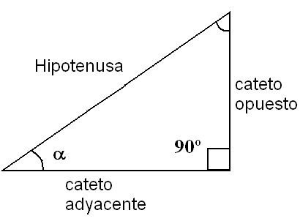
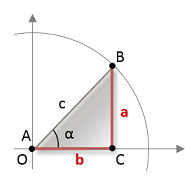
En un triángulo rectángulo la tangente de un ángulo es una razón trigonométrica que se puede definir geométricamente como el cateto opuesto sobre el cateto adyacente
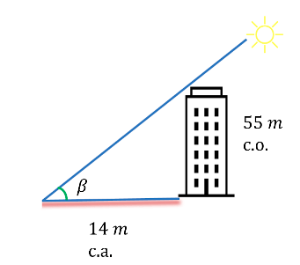
Por ejemplo, si un edificio de 55 metros de altura proyecta una sombra de 14 metros, se puede calcular la tangente del ángulo
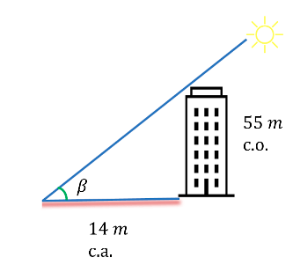
En este caso el cateto opuesto del ángulo es la altura del edificio, mientras que el adyacente es la distancia hasta la base del edificio.
El valor del ángulo será la inversa de la tangente, es decir, buscamos el ángulo cuya tangente es igual a 3.93. Esto es lo mismo que buscar la tangente inversa o arcotangente de 3.93.
Actividad 1
Repetir el ejemplo anterior para calcular el ángulo suponiendo ahora que la sombra del edificio es de 4 metros. ¿Cual será el valor de ?
A medida que el sol se aleja del horizonte y sube, la sombra se va haciendo más pequeña, hasta que llega a ser cero cuando el sol está justo sobre el edificio, es decir, el ángulo que forma es de 90 grados.
Suponiendo que en el sistema de referencia de la hoja dinámica el monumento tiene una altura de 4 unidades, si se conoce el ángulo se puede calcular la sombra del monumento usando la tangente.
La tangente del ángulo será el cateto opuesto, es decir, la altura del monumento, entre el cateto adyacente, que será la sombra que proyecta sobre el suelo.
Se puede pulsar el botón inferior derecho para iniciar la animación del movimiento del sol.
Actividad 2
Utilizar la hoja dinámica anterior para encontrar el ángulo cuya sombra es igual a 8.35
Actividad 3
Calcular el ángulo para el cual la sombra será igual a la altura del monumento, es decir, igual a 4