reactie van Euler
Een eerste reactie
Euler vindt het maar niets en antwoord aan de burgemeester:
"... U ziet dus, weledele Heer, dat dit problem weinig met wiskunde te maken heeft en ik begrijp niet waarom U van een wiskundige verwacht om het op te lossen in plaats van iemand anders, want de oplossing is enkel gebaseerd op redeneervermogen en op geen enkel wiskundig principe. Daarom begrijp ik niet waarom zelfs problemen die zo weinig met wiskunde te maken hebben sneller opgelost worden door wiskundigen dan door anderen."
triviaal en toch intrigerend...
Ook al vond Euler het een triviaal probleem, het blijft hem bezighouden en hij schrijft in een brief aan een Italiaanse wiskundige en ingenieur:
"De vraag is zo banaal, maar het valt op te merken dat noch de meetkunde, noch de algebra volstaat om het op te lossen."
Euler vermoedt dat het probleem verband houdt met een onderwerp dat Leibnitz 'geometrie van positie' noemde. En wat doet een wiskundige dan? Hij veralgemeent het probleem en ontwikkelt een wiskundig model dat de start zou zijn van een nieuwe tak van de wiskunde die we nu niet meer 'geometrie van positie' noemen, maar topologie.
Hoe begin je aan een probleem?
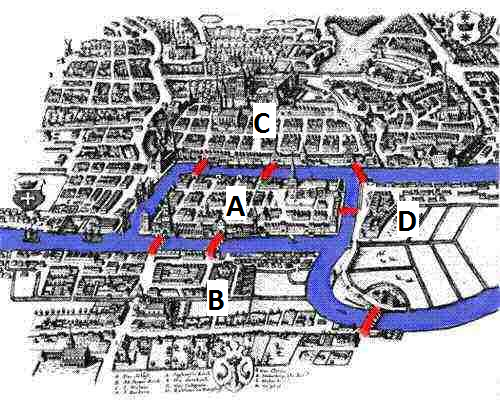
Als wiskundige weet Euler dat je een probleem best veralgemeent. Je spreekt dus niet langer over een wandeling waarbij je de namen van de twee eilanden of de bruggen gebruikt, maar ziet dat de rivier de stad verdeelt in vier delen A, B, C en D met daartussen 7 verbindingen. Ga je over een brug van stadsdeel A naar stadsdeel B, dan schrijf je dat gewoon als AB. Ga je van A naar B en neem je daarna een tweede brug naar C en tenslotte een derde naar D, dan schrijf je dat als ABCD. Hij ziet meteen dat je één letter meer nodig hebt dan het aantal bruggen dat je oversteekt. Met andere woorden: om zeven bruggen over te steken heb je 8 letters nodig. Euler is de eerste die dergelijk probleem systematisch onderzoekt.
Anderhalve eeuw later, in 1878 introduceert J.J. Sylvester de grafische weergave van zulke verbindingen. En zo belanden we bij wat we nu een graaf noemen: een voorstelling met punten, waarvan sommige door lijnen met elkaar verbonden zijn.
Het bruggenprobleem is nu herleid tot de vraag 'welke grafen hebben welke eigenschappen?'.