Concepto de logaritmo
1. Definición de logaritmo
El logaritmo en base b de un número a se representa por logb(a) y es el número c que cumple bc = a:
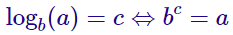
- El número b es la base del logaritmo. Tiene que ser un real positivo distinto de 1.
- El número a es el argumento del logaritmo.
- El número c es el logaritmo en base b de a.
Ejemplos
2. Cálculo de logaritmos
Logaritmo 1
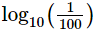 Solución:
Recordad que el exponente negativo es la inversa de una fracción. La fracción puede escribirse como una potencia negativa de 10:
Solución:
Recordad que el exponente negativo es la inversa de una fracción. La fracción puede escribirse como una potencia negativa de 10:
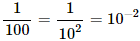 Por tanto, el logaritmo es
Por tanto, el logaritmo es
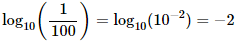 Logaritmo 2
Logaritmo 2
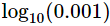 Solución:
El número decimal 0.001 es la potencia -3 de 10 (el exponente es el número de ceros). Por tanto,
Solución:
El número decimal 0.001 es la potencia -3 de 10 (el exponente es el número de ceros). Por tanto,
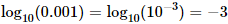 Logaritmo 3
Logaritmo 3
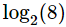 Solución:
Como 2 al cubo es 8,
Solución:
Como 2 al cubo es 8,
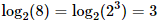 Logaritmo 4
Logaritmo 4
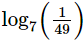 Solución:
Como 49 es 7 al cuadrado, la fracción del argumento del logaritmo es 7 elevado a -2 y, por tanto, el logaritmo es
Solución:
Como 49 es 7 al cuadrado, la fracción del argumento del logaritmo es 7 elevado a -2 y, por tanto, el logaritmo es
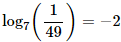 Logaritmo 5
Resolver la siguiente ecuación logarítmica (hallar x):
Logaritmo 5
Resolver la siguiente ecuación logarítmica (hallar x):
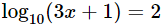 Solución:
La base del logaritmo es 10. El logaritmo es 2.
Aplicando la definición del logaritmo, 10 elevado a 2 tiene que ser igual al argumento del logaritmo:
Solución:
La base del logaritmo es 10. El logaritmo es 2.
Aplicando la definición del logaritmo, 10 elevado a 2 tiene que ser igual al argumento del logaritmo:
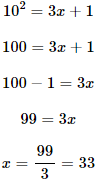 Más ejercicios similares en concepto y cálculo de logaritmos.
Más ejercicios similares en concepto y cálculo de logaritmos.
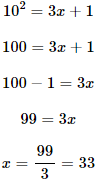 Más ejercicios similares en concepto y cálculo de logaritmos.
Más ejercicios similares en concepto y cálculo de logaritmos.