Asíntota del toro
Son las trayectorias de un móvil que se mueve en la superficie para que el vector de aceleración esté en todo momento en el plano tangente a la superficie.
Siendo M(u,w) la función vectorial asociada a la superficie y N(u,v) el vector normal a la misma en cada punto, la ecuación diferencial de la asíntota es
d²M · N = 0 ⇔ dM · dN = 0
Para el toro de ecuaciones
x = (R +r cos(w)cos(u)
y = (R +r cos(w)sen(u)
z = r sen(w)
Se obtienen las ecuaciones diferenciales
(R + r cos(w))cos(w) du² +r dw² = 0
En el caso de ser r = R se obtiene
du² = r / (r(1 + cos(w))cos(w)) dw² ⇒ du = ± 1/ sqrt((1 + cos(w))cos(w)) dw
Lo que lleva a una integral elíptica si bien resoluble en este caso:
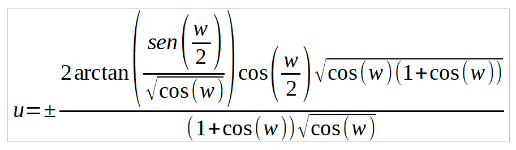
A partir de aquí pueden obtenerse las ecuaciones paramétricas:
x = ±2r cos(t) / (1 + cosh²(t / sqrt(2)))
y = 2r sen(t) / (1 + cosh²(t / sqrt(2)))
z = 2r cosh(t / sqrt(2)) / (1 + cosh²(t / sqrt(2)))
Se trata por tanto de un par de curvas simétricas respecto al plano OYZ, cerradas y con una autointersección.