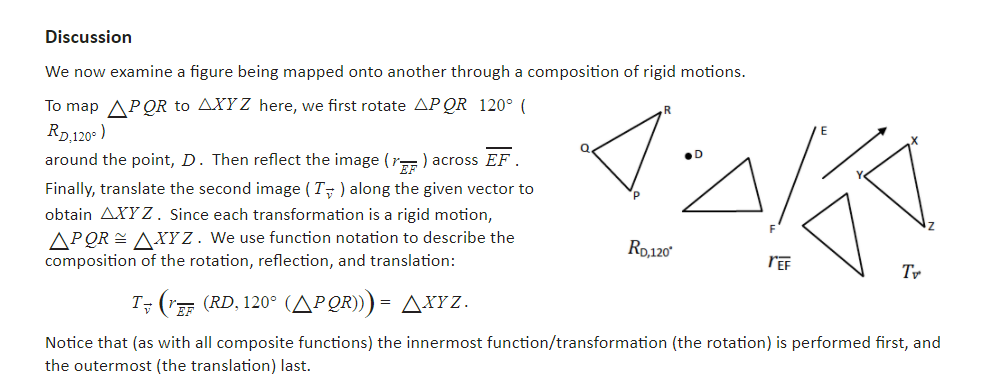
C7 Construct and Apply a Sequence of Rigid Motions
We have been using the idea of congruence already (but in a casual and unsystematic way). In Grade 8, we introduced and experimented with concepts around congruence through physical models, transparencies, or geometry software. Specifically, we had to
(1) Understand that a two-dimensional figure is congruent to another if the second can be obtained from the first by a sequence of rotations, reflections, and translations; and (2) describe a sequence that exhibits the congruence between two congruent figures. (8.G.A.2)
As with so many other concepts in high school Geometry, congruence is familiar, but we now study it with greater precision and focus on the language with which we discuss it.
Let us recall some facts related to congruence that appeared previously in this unit.
- We observed that rotations, translations, and reflections—and thus all rigid motions—preserve the lengths of segments and the measures of angles. We think of two segments (respectively, angles) as the same in an important respect if they have the same length (respectively, degree measure), and thus, sameness of these objects relating to measure is well characterized by the existence of a rigid motion mapping one thing to another. Defining congruence by means of rigid motions extends this notion of sameness to arbitrary figures, while clarifying the meaning in an articulate way.
- We noted that a symmetry is a rigid motion that carries a figure to itself.
Add three main ideas from the reading:
Notes (if any):
