Einheitskreis und Sinusfunktion
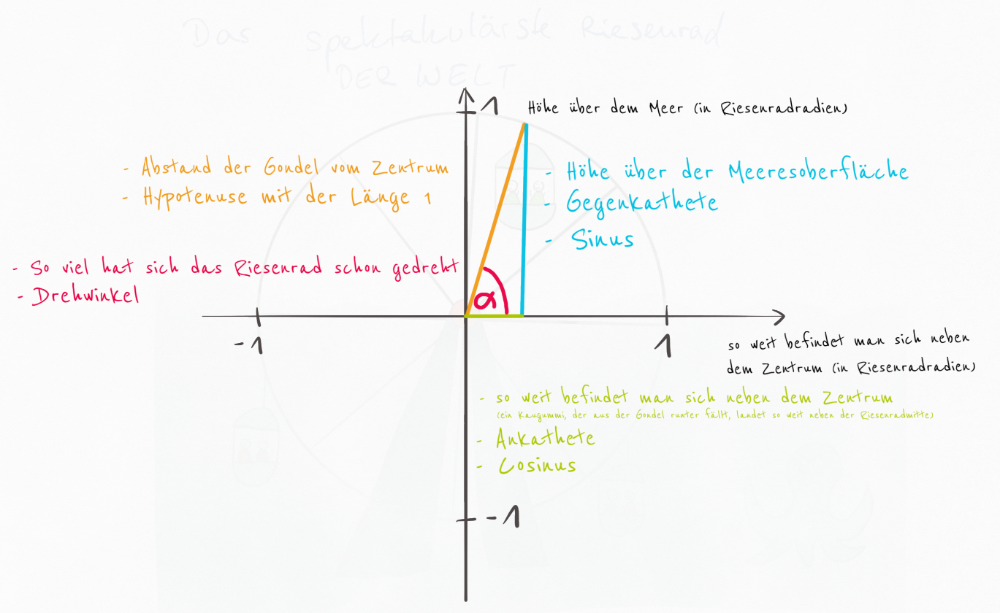
Betrachtet man nur Rechtwinklige Dreiecke, kann man den Sinus, Cosinus und Tanges nur für Winkel, die maximal 90° groß sind, bestimmen. Um nun auch einen Wert für andere Winkel zu bestimmen, benötigt man einen phänomenalen, hirnverdrehenden Trick: Man nutzt dazu ein Dreieck mit der Hypothenusenlänge 1.
Mit sin(α) = kann man den Wert von sin (α) direkt ablesen.
Mit cos(α) = kann man den Wert von cos(α) direkt ablesen.
1. Weg: Der Einheitskreis
Für einen konkreten Winkel kann man damit die Werte für den Sinus und Cosinus direkt ablesen. Hier im Beispiel siehst du α = 30° mit sin(30°) = 0,5 und cos(30°) = 0,87
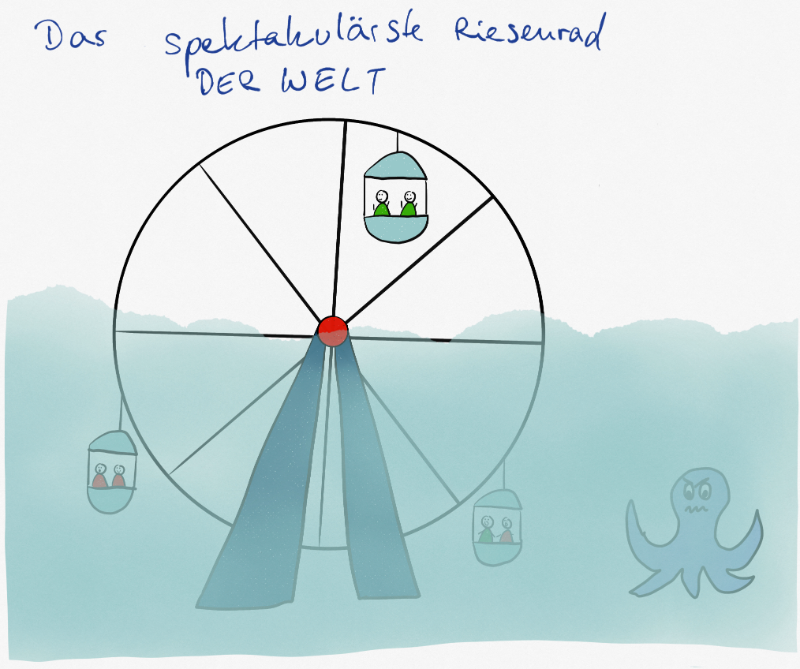
2. Weg: Das spektakulärste Riesenrad der Welt
Etwas actionreicher kannst du dir die ganze Situation am verrrücktesten, spektakulärsten Riesenrad der Welt vorstellen: Es sei im Wasser gebaut, seine obere Hälfte schaue aus dem Meer heraus, in der unteren Hälfte befinde es sich unter Wasser. (Es ist ein wirklich spektakuläres Gedankenexperiment!)
Auch hier setzt man die Länge der Hypotenuse (Also den Radius des Riesenrads) auf 1. Man könnte z.B. sagen, es hat den Radius von einer Riesenradbreite. Einheiten sind in Gedankenexperimenten zum Glück meist eh nicht wichtig… Hier gibt es wieder genau eine Größe, von der alles abhängt: Der Winkel α, der angibt, wie weit sich das Riesenrad schon gedreht hat.
- sin(α) ist dann die Höhe, in der sich eine Gondel über der Meeresoberfläche befindet,
- cos(α) gibt an, wie dicht neben dem Zentrum des Riesenrads ein Kaugummi landen würde, den du aus der Gondel heraus fallen lässt.
Überlege dir, wie die Abbildung aussehen müsste, damit du sin(0°) und cos(0°), sin(90°) und cos(90°) sowie sin(60°) und cos(60°) ablesen kannst.
Du findest weiter unten eine Animation, mit der du deine Lösung überprüfen kannst.
Einige Sinus- und Cosinus-Werte kann man nun vom Kreis ablesen, z.B.
- sin(0°)
- sin(90°)
- cos(0°)
- cos(90°)
- sin(60°)
- cos(60°)
Überprüfe deine Überlegungen für die genannten Sinus- und Cosinus-Werte
Damit kann man für beide Funktionen eine erste Wertetabelle füllen:

 Aus dieser Wertetabelle ergeben sich erste Punkte für den Graph der jeweiligen Funktionen.
Aus dieser Wertetabelle ergeben sich erste Punkte für den Graph der jeweiligen Funktionen.
Aufgabe
Zeichne dir einen Einheitskreis mit einem Radius von 10cm = 1dm ("Dezimeter") ((höchste Zeit, den Zirkel mal wieder rauszukramen ;o) Und: Lege das Blatt im Querformat an))
Nun kannst du selber beliebige Sinus- und Cosinus-Werte ermitteln. Beachte, dass du in dm messen musst, d.h. hat deine Gegenkathete die Länge 5cm, entspricht dies 0,5dm und damit einem Sinus von 0,5.
Ermittle mit Hilfe deines Einheitskreises folgende Werte
Aufgabe
Übertrage deine Werte in ein von dir gezeichnetes Koordinatensystem. Auf der x-Achse trägst du dabei die Winkel ab. Wähle deine Einteilung so, dass du Winkel von -90° bis 400° einzeichnen kannst.
…Weiter geht es…
Nun kannst du dich schon etwas auf dem Einheitskreis bewegen. Überlege dir
- wie das Dreieck aussehen könnte, wenn α > 90° ist (Beachte, dass die Hypotenuse immer noch die längste Seite sein muss)
- wie das Dreieck aussehen könnte, wenn α > 180° ist
- wie das Dreieck für α > 360° aussehen könnte
- wie das Dreieck für α < 0° aussehen könnte