Daire ve daire diliminin alanı M.7.3.3.3.
GİRİŞ=

Yukarıdaki etkinliklerden dairenin alanının bulunmasında hangi geometrik şeklin alanından yararlandık ? Daire diliminin alanının, daire dilimini gören merkez açıyla bir ilişkisi var mıdır ? Matematiksel ifadeyle ne söylenebilir ? açıklayınız.
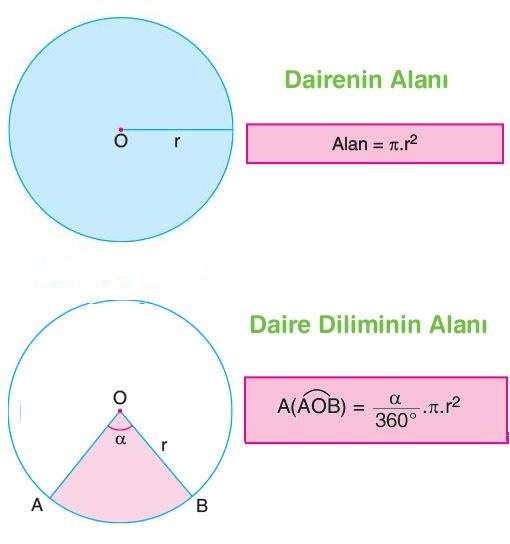
 A=π.r2.α/360 formülüyle bulunur. Bu formülde α yerine merkez açı ölçüsünü, r yerine yarıçap ölçüsünü, π yerine de π sayısını yazarız. Aslında daire diliminin alanı; dairenin alanının merkez açı kadarlık parçasını bulmaktır.
A=π.r2.α/360 formülüyle bulunur. Bu formülde α yerine merkez açı ölçüsünü, r yerine yarıçap ölçüsünü, π yerine de π sayısını yazarız. Aslında daire diliminin alanı; dairenin alanının merkez açı kadarlık parçasını bulmaktır.Yarıçaplar değiştirdikçe büyük ve küçük daire halkasının alanları nasıl değişti ? açıklayınız.

Emekli olan Öğretmen İbrahim Bey’e, arkadaşları hizmet anısı olarak yandaki gibi daire biçiminde bir plaket verdiler. Bu plaketin alanı 108 cm2 olduğuna göre yarıçapının uzunluğunu bulalım (π = 3 alalım.)
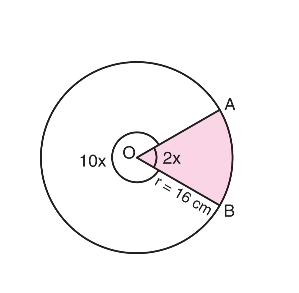
Yukarıdaki şekilde verilenlere göre boyalı bölgenin alanını bulunuz (π = 3 alınız.)
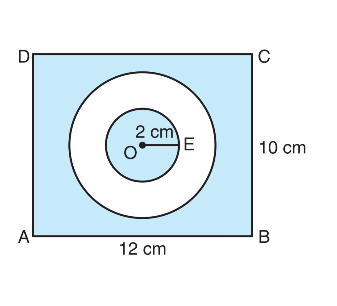
Yukarıdaki ABCD dikdörtgeninin iç bölgesinde O merkezli iki tane çember çizilmiştir. |AB| = 12 cm, |BC| = 10 cm, |OE| = 2 cm’dir ve büyük çemberin yarıçap uzunluğu, küçük çemberin yarıçap uzunluğunun 2 katıdır. Boyalı bölgelerin toplam alanını bulunuz (π = 3 alınız.)