Image d'un triangle par une homothétie
Partie A Je construis
Construis un triangle ABC et un point O.
Boutons à utiliser : 
et 
et Crée un nombre k, variant de 0 à 5.
Aide : Sélectionne le bouton curseur 
, puis clique sur la zone graphique, et enfin, saisis 0 pour min et 5 pour max.
, puis clique sur la zone graphique, et enfin, saisis 0 pour min et 5 pour max.Positionne le curseur sur k = 2.
Construis le point A', image du point A par l'homothétie de centre O et de rapport k.
Aide : Sélectionne le bouton homothétie 
, puis sélectionne le point A, puis le point O, et enfin, saisis le rapport de l'homothétie : k.
, puis sélectionne le point A, puis le point O, et enfin, saisis le rapport de l'homothétie : k.De même, construis les points B' et C', images respectives des points B et C par l'homothétie de centre O et de rapport k.
Partie B Je verbalise (homothétie de rapport positif)
Trace le triangle A'B'C'. Comment semblent être les triangles ABC et A'B'C' ?
Trace les droites (AA'), (BB') et (CC').
Bouton à utiliser : 
Que peux-tu dire de ces trois droites ?
Si k > 1 :
Si k = 1 :
Si 0 < k < 1 :
Calcule le quotient dans la cellule A1 du tableur.
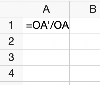
Calculer le quotient dans la cellule A2 du tableur.
Calculer le quotient dans la cellule A3 du tableur.
Ces trois quotients sont-ils égaux ? Si oui, à quoi correspond cette valeur ?
Partie C Je verbalise (homothéties de rapport positif et négatif)
Crée un nombre k', variant de -5 à 0.
Construis les points A'1, B'1 et C'1, images respectives des points A, B et C par l'homothétie de centre O et de rapport k'.
Positionne le curseur sur k = -2.
Si 0 < k < 1 :
Si k < -1 :
Si k = -1 :
Partie D Je conjecture les étapes de constructions sur papier
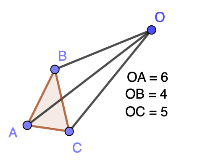
On souhaite construire le triangle A'B'C', image du triangle ABC par l'homothétie de centre O et de rapport -2. Calculer OA', OB' et OC'.
Sur la zone graphique ci-dessous, construire le triangle A'B'C', image du triangle ABC par l'homothétie de centre O et de rapport -2.
Mesure les longueurs OA', OB' et OC'. Puis, vérifie qu'elles correspondent aux résultats trouvés à la question précédente.