Exponential and logistic growth
Key points
- In exponential growth, a population's per capita (per individual) growth rate stays the same regardless of population size, making the population grow faster and faster as it gets larger.
- In nature, populations may grow exponentially for some period, but they will ultimately be limited by resource availability.
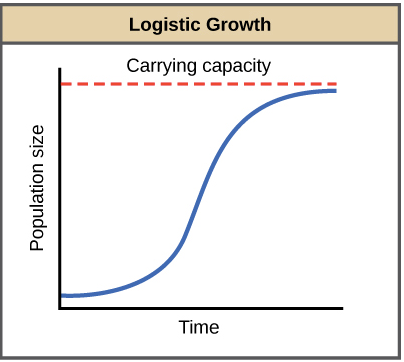
- In logistic growth, a population's per capita growth rate gets smaller and smaller as population size approaches a maximum imposed by limited resources in the environment, known as the carrying capacity.
- Exponential growth produces a J-shaped curve, while logistic growth produces an S-shaped curve.
Introduction
In theory, any kind of organism could take over the Earth just by reproducing. For instance, imagine that we started with a single pair of male and female rabbits. If these rabbits and their descendants reproduced at top speed ("like bunnies") for 777 years, without any deaths, we would have enough rabbits to cover the entire state of Rhode Island. And that's not even so impressive – if we used E. coli bacteria instead, we could start with just one bacterium and have enough bacteria to cover the Earth with a 111-foot layer in just 36 hours!
As you've probably noticed, there isn't a 111-foot layer of bacteria covering the entire Earth (at least, not at my house), nor have bunnies taken possession of Rhode Island. Why, then, don't we see these populations getting as big as they theoretically could? E. coli, rabbits, and all living organisms need specific resources, such as nutrients and suitable environments, in order to survive and reproduce. These resources aren’t unlimited, and a population can only reach a size that match the availability of resources in its local environment.
Population ecologists use a variety of mathematical methods to model population dynamics (how populations change in size and composition over time). Some of these models represent growth without environmental constraints, while others include "ceilings" determined by limited resources. Mathematical models of populations can be used to accurately describe changes occurring in a population and, importantly, to predict future changes.
Exponential growth
Bacteria grown in the lab provide an excellent example of exponential growth. In exponential growth, the population’s growth rate increases over time, in proportion to the size of the population.Let’s take a look at how this works. Bacteria reproduce by binary fission (splitting in half), and the time between divisions is about an hour for many bacterial species. To see how this exponential growth, let's start by placing 100010001000 bacteria in a flask with an unlimited supply of nutrients.
- After 111 hour: Each bacterium will divide, yielding 200020002000 bacteria (an increase of 100010001000 bacteria).
- After 222 hours: Each of the 200020002000 bacteria will divide, producing 400040004000 (an increase of 200020002000 bacteria).
- After 333 hours: Each of the 400040004000 bacteria will divide, producing 800080008000 (an increase of 400040004000 bacteria).

Logistic growth
Exponential growth is not a very sustainable state of affairs, since it depends on infinite amounts of resources (which tend not to exist in the real world).Exponential growth may happen for a while, if there are few individuals and many resources. But when the number of individuals gets large enough, resources start to get used up, slowing the growth rate. Eventually, the growth rate will plateau, or level off, making an S-shaped curve. The population size at which it levels off, which represents the maximum population size a particular environment can support, is called the carrying capacity, or KKK.