Calculer une longueur grâce au Théorème de Thalès
Cette activité suit l'activité que vous découvrirez ci-dessous :
Découvrir la propriété de Thalès
Si vous avez déjà suivi cette activité, vous pouvez passer à la suite;
(Dans toute cette activité, vous utiliserez le . du clavier numérique pour les nombres décimaux.)
Nous allons maintenant nous entraîner à calculer des longueurs grâce au Théorème de Thalès :
Quelles semblent être les droites parallèles ? Vous pourrez utiliser l'outil "relation" de la figure pour que Géogebra vérifie que votre affirmation est vraie !
Compléter la démonstration suivante. (les cases oranges)
Grâce au tableau de proportionnalité suivant, calculez les longueurs CE et CG. Vous compléterez les cases oranges avec des valeurs relevées sur la figure, puis les cases violettes avec des formules de tableur :
Quelle est la valeur de CG ?
(Vous donnerez votre résultat sans unité)
Exemple 2 :
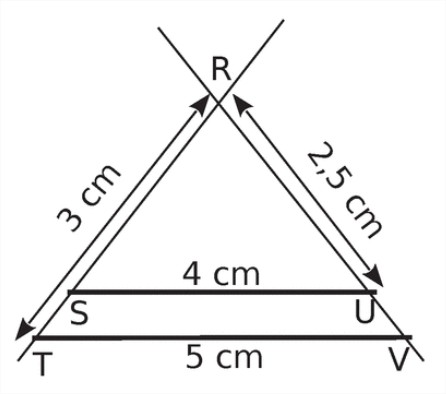
Grâce à ce tableur, calcule la longueur RS :
La longueur RS est égale à
Vous donnerez le résultat sans unité
Exemple 3
Soit EFG un triangle tel que EF = 5cm; EG = 4cm et FG = 3,3 cm.
On appelle M le point de [EG) tel que EM = 6cm.
Trace la parallèle à (FG) passant par M. Elle coupe [EF) en N.
Si besoin vous pouvez réviser comment construire un triangle avec cette vidéo.
Faire la figure dans geogebra :
Grâce à ce tableur, calcule la longueur EN :
La longueur EN est égale à
Vous donnerez le résultat sans unité