Monotonie von Funktionen
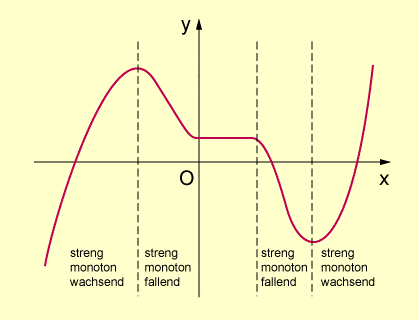
Graphen von Funktionen können in bestimmten Intervallen steigen, fallen oder parallel zur x-Achse verlaufen.
Steigt der Graph, so wachsen die Funktionswerte, d.h., für x1<x2
ist auch f(x1)<f(x2)
In diesem Fall heißt die Funktion in dem betrachteten Intervall streng monoton wachsend. Ist das nicht nur in einem bestimmten Intervall, sondern im gesamten Definitionsbereich Df der Fall, so heißt die Funktion streng monoton wachsend.
Gilt dagegen
für f(x1)>f(x2) für x1<x2 dann spricht man von streng monoton fallend.
Didaktischer Kommentar
Die geplante Stunde „Monotonie der Funktionen “ ist Teil einer umfangreichen Unterrichtsreihe zu den Themen Funktionen.
Die Schüler sollten umfassendes Vorwissen über die Funktionen wissen und mit allen Begriffen von Funktionen wie x-Achse, y-Achse, etc. vertraut sein. Für eine schnelle und zielgerichtete Erarbeitung der Stundeninhalte wären zudem grundlegende Kenntnisse über den Funktionsgraph notwendig.
Wir betrachten in dieser Unterrichtseinheit die Monotonie der Funktionen. Die Schülerinnen und Schüler sollen ein Gespür für das Monotonieverhalten einer Funktion erhalten.