Gauss Triag-Diag-Subst CAS Funktionen
Gauss-Schritte über CAS Funktionen
Die Ausgangsmatrix und die Zwischenschrittmatrizen so ausrichten, dass die Diagonalelemente besetzt sind - ggf. Zeilentausch durchführen. Tzs-Tauschfunktion in Werkzeugkiste (Buch CAS 4 lineare Gleichungen). Wenn sich 0-Zeilen ergeben tauschen sie diesen nach "unten".
 Keep Input" abschließen!
Keep Input" abschließen!
GaussTriag(A,s)
- Spalte s, Elemente unterhalb der Diagonalen von A auf 0 setzen (s=1..n-1)
- Obere Dreiecksmatrix durch Zeilenumformungen erzeugen
- Führen sie GausTriag-Schritte durch bis alle Elemente (Spalte 1..n-1) unter der Diagonalen 0 sind
GaussTriag(MM,zz):=Sequence(If(kk>zz,Element(MM,kk) - Element(MM,kk,zz)/Element(MM,zz,zz)*Element(MM,zz),Element(MM,kk)) ,kk,1,Length(MM))
|
| |||||||||
GaussDiag(A)
- Diagonal-Elemente von A auf 1 setzen
- GaussSubst benötigt eine Diagonale aus 1en
GaussDiag(MM):=Sequence(If(Element(MM,kk,kk)<>0, Element(MM,kk)/Element(MM,kk,kk),Element(MM,kk)),kk,1,Length(MM))
|
| |||||||||
GaussSubst(A,s)
- Spalte s, Elemente überhalb der Diagonalen von A auf 0 setzen (s=n..2)
- Obere Dreiecksmatrix durch Zeilenoperationen zur Einheitsmatrix umformen
- Wenden sie GaussSubst von Spalte n...2 an bis sie die Einheitsmatrix, Identity(n), erhalten
GaussSubst(MM,zz):=Sequence(If(kk<zz,Element(MM,kk)-Element(MM,kk,zz)Element(MM,zz),Element(MM,kk)),kk,1,Length(MM));
|
|
Tzs(zz,ss,nn):=Sequence(Sequence( If((zz==kk ∧ ss==jj) ∨ (ss==kk ∧ zz==jj) ∨ (kk==jj ∧ kk≠zz ∧ jj≠ss) ,1,0),kk,1,nn),jj,1,nn);
Die Argumente der Funktionen sind MM (Matrix) und zz (Zeile) - immer verdoppelt um Überschneidungen mit anderen Namen im CAS- oder Algebra-Fenster zu vermeiden. Auch die Laufvariable kk nicht nochmal verwenden! Wenn sie die Funktionen GaussTriag, GaussDiag, GaussSubst in ein eigenes Applet übernehmen die Definitionen mit "Behalte Eingabe  Keep Input" abschließen!
Keep Input" abschließen! 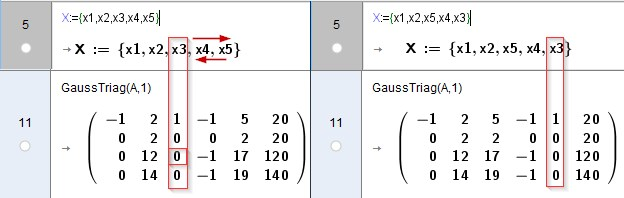
Im Applet ist auch im Lösungsvektor x3 <==> x5 getauscht - verwende Tauschmatrix Tzs um die Standard-Reihenfolge herzustellen:
Tzs(3,5,nx)Transpose(X) = Tzs(3,5,nx)Transpose(Substitute(X_{L},$20))
Beispiel:
LGS mit Parameter a
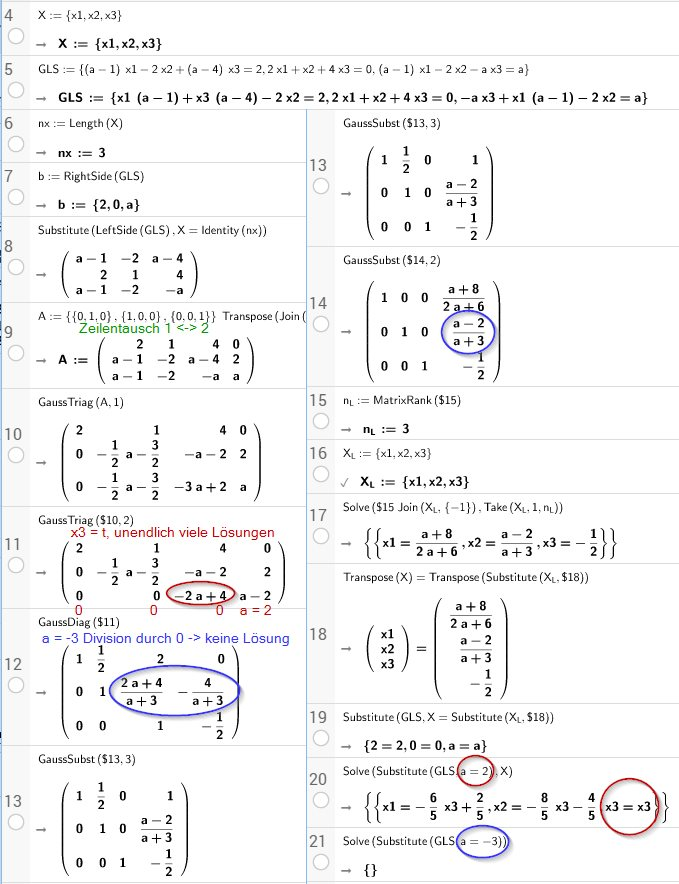
GLS:={(a-1)x1-2x2+ (a-4)x3=2,2x1+x2+4x3=0,(a-1)x1-2x2-a*x3=a}
oder mit Spaltentausch 1<->2
GLS:={(a-1)x1-2x2+ (a-4)x3=2,2x1+x2+4x3=0,(a-1)x1-2x2-a*x3=a} {{0, 1, 0}, {1, 0, 0}, {0, 0, 1}}