Proporción áurea
NOTA INICIAL
Ejercicio 17 del CURSO DE INICIACIÓN A GEOGEBRA
Primero de una serie de ejercicios vinculados entre sí, que toman como base el n° φ (phi) y la temática proporción áurea
Se busca aquí dividir un segmento dado, de manera que los segmentos resultantes cumplan:
"La sección áurea de un segmento AB dado es otro segmento AF, fruto de su división, de tal manera que la relación entre el segmento mayor dado (AB) y el mediano resultante de la división (AF), sea la misma que la relación entre el mediano (AF) el pequeño resultante (FB). (El pequeño es al mediano lo mismo que el mediano al mayor)."
| El método empleando regla y compás puede verse en la siguiente imagen | 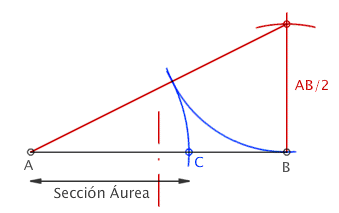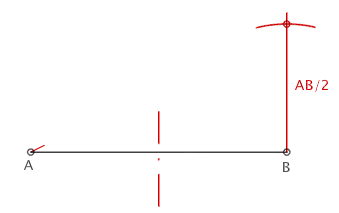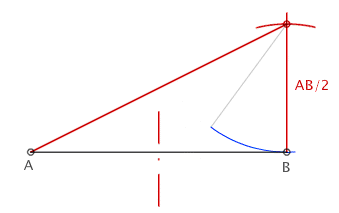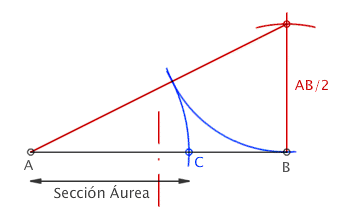 |
Protocolo de Construcción
Tratamos de dividir un segmento de una longitud cualquiera en otros dos que estén en proporción áurea. Para ello dibujamos un triángulo rectángulo cuyos catetos tengan longitud a y a/2.
- Usando
 dibujamos un punto A.
dibujamos un punto A. - Con la herramienta
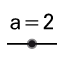 insertamos un deslizador de Valor mínimo 1, Valor máximo 10 e Incremento 1. Fijamos el valor en 7 con la herramienta Elige y Mueve.
insertamos un deslizador de Valor mínimo 1, Valor máximo 10 e Incremento 1. Fijamos el valor en 7 con la herramienta Elige y Mueve. - En la barra de entrada escribimos
(x(A), y(A) + a). Ya tenemos el vértice B. - En la barra de entrada escribimos
(x(B) + a/2, y(B)). Ya tenemos el vértice C. - Dibujamos el triángulo de vértices A, B y C con la herramienta polígono
 .
.
- Usando
 trazamos la circunferencia d con centro en C que pasa por B.
trazamos la circunferencia d con centro en C que pasa por B.
- Hallamos el punto de corte, D, de la hipotenusa del triángulo ABC con la circunferencia d.
- Trazamos la circunferencia e con centro en A que pasa por D empleando
 .
. - Hallamos el punto de corte, E, del cateto AB con la circunferencia e.
- Los segmentos AE y BE están en proporción áurea. Para comprobarlo insertamos un texto que calcule el cociente entre ambos segmentos... en el comando Redondeo del menú Configuración... seleccionamos 10 Lugares decimales y desplazamos el deslizador para ver que el cociente no cambia.
Cálculo gráfico de la sección áurea (búsqueda del punto dorado de un segmento)
Imagen referenciada