Η δυναμική τής Ευκλείδειας Γεωμετρίας στην εννοιολογική κατανόηση της συνάρτησης
Πρόλογος
Η παρούσα δραστηριότητα χρησιμοποιήθηκε για την πειραματική διδασκαλία που παρουσιάσαμε σε μαθητές τής Α΄ Λυκείου στα πλαίσια διοργάνωσης του Μαθη(μα)τικού Συμποσίου .
Αθήνα 5/4/2025 - Διοργάνωση: Σύμβουλοι Μαθηματικών Δ.Ε, Περιφερειακή Διεύθυνση Δ.Ε Αττικής - ΙΕΠ
Παρουσίαση: Μ. Τσιλπιρίδης

Οδηγίες
Στο ψηφιακό δόμημα περιέχονται:
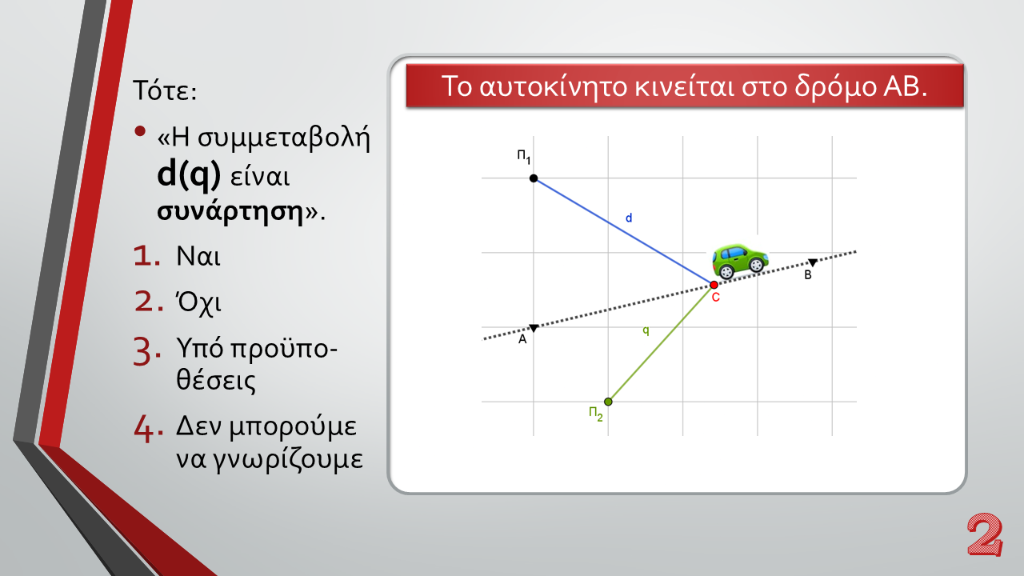
- Το σημείο "Αυτοκίνητο" που μετακινεί το αυτοκίνητο κατά μήκος της διαδρομής ΑΒ.
- Τα σημεία Α, Β και "Πόλη" τα οποία μετακινούνται ελεύθερα

