Arnaud Durand - Démonstration du théorème de Pythagore
Que pouvons-nous dire des trois triangles obtenus par rapport au triangle de départ ?
Nous allons réagencer ces trois triangles rectangles. Pour cela, cliquer à nouveau à trois reprises sur le bouton SUIVANT. Quelle semble être la nature du polygone obtenu ?
Dans le triangle initial, que pouvons-nous dire de la somme des mesures des trois angles ?
Que pouvons-nous en déduire pour la somme des mesures de l'angle rouge et de l'angle vert ?
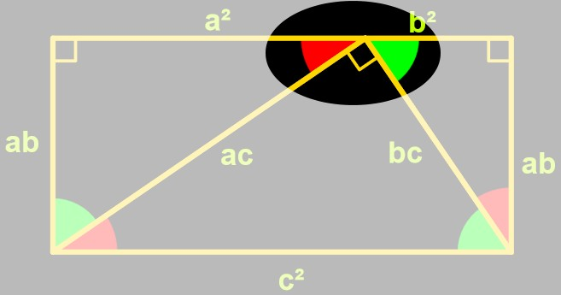
Dans cette partie de la figure, nous avons un angle droit, un angle rouge et un angle vert. Quelle est donc la valeur de l'angle formé par ces trois angles ?

Dans cette partie de la figure, nous avons un angle rouge et un angle vert. Quelle est donc la mesure de l'angle formé par ces deux angles ?
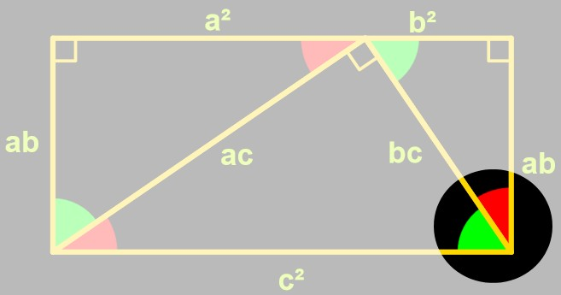
Dans cette partie de la figure, nous avons un angle rouge et un angle vert. Quelle est donc la mesure de l'angle formé par ces deux angles ?
Le polygone créé est ainsi un quadrilatère possédant quatre angles droits. Quelle est sa nature ?
Le quadrilatère étant un rectangle, que pouvons-nous dire des longueurs de ses côtés opposés ?
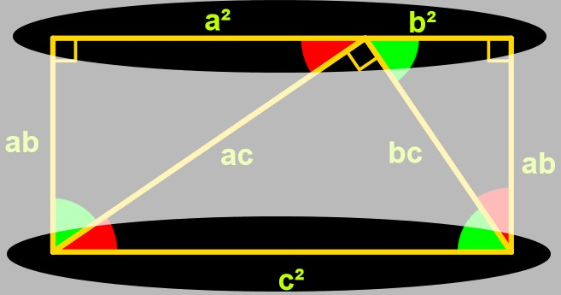
En déduire une égalité entre a, b et c.