ATIVIDADE 1 – TRANSFORMAÇÕES ISOMÉTRICAS
Transformações isométricas
Isometria é uma palavra que tem origem grega da palavra isometría, composta pelos termos
iso (igual) e metron (medida), logo podemos entender a origem como sendo “igual medida” ou “igualdade de medida”.
Na matemática, uma isometria é uma transformação geométrica que mantém a distância
e os ângulos de uma figura, ou seja, que preserva as medidas das figuras
geométricas.
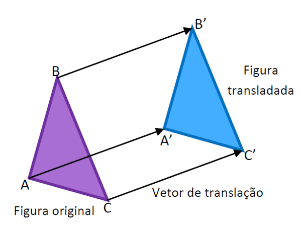
Translação
A palavra translação vem do Latim “vehere” que significa transportar. A transformação em que a imagem é
obtida pelo deslocamento paralelo de todos os pontos em uma mesma distância,
direção e sentido é denominada translação. Logo, pela definição, mantem-se o
tamanho da figura e sua forma.
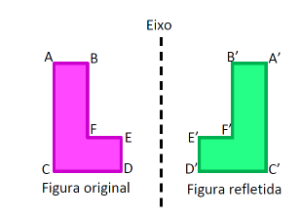
Reflexão
A reflexão é uma simetria, pois é uma transformação que considera a distância do conjunto de
pontos a uma reta e com essa distância reflete a figura no outro lado da reta – também chamada de eixo de simetria.
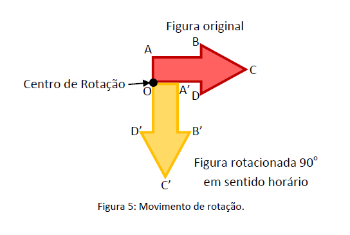
Rotação
A rotação é uma transformação que gira a imagem em torno de um ponto fixo – centro de rotação –considerando uma amplitude (ângulo da rotação).
Como fazer transformações isométricas no GeoGebra
Vamos aprender agora como criar as transformações no plano.
Translação
Leia com atenção as instruções e faça na Janela do GeoGebra disponível abaixo.

Translação
Reflexão
Para fazer uma reflexão no plano, precisa-se em ordem:

Reflexão
Rotação
Para fazer uma Rotação no plano, precisa-se em ordem:
