Aula invertida: Estimaciones para determinar áreas bajo la curva
Actividad 1. Área bajo la curva, casos particulares
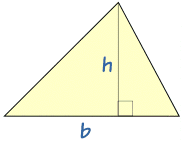 Áreas de polígonos regulares
Para calcular el área de un polígono regular cualquiera se divide en triángulos uniendo el centro
con cada uno de los vértices. La altura de cada uno de los triángulos coincide con la apotema del
polígono. Se calcula el área de uno de estos triángulos y se multiplica por el número de triángulos
que se han formado.
Áreas de polígonos irregulares
Para calcular el área de un polígono irregular cualquiera debemos basarnos en métodos indirectos.
Estos métodos, básicamente, son tres: el llamado método de triangulación, el uso de una trama
cuadriculada o, en algunos casos, descomponer el polígono en cuadriláteros conocidos.
Áreas de polígonos regulares
Para calcular el área de un polígono regular cualquiera se divide en triángulos uniendo el centro
con cada uno de los vértices. La altura de cada uno de los triángulos coincide con la apotema del
polígono. Se calcula el área de uno de estos triángulos y se multiplica por el número de triángulos
que se han formado.
Áreas de polígonos irregulares
Para calcular el área de un polígono irregular cualquiera debemos basarnos en métodos indirectos.
Estos métodos, básicamente, son tres: el llamado método de triangulación, el uso de una trama
cuadriculada o, en algunos casos, descomponer el polígono en cuadriláteros conocidos.
Resuelve el siguiente ejercicio usando la información anterior.
Una empresa fabrica sombrillas para la playa. Para ello usa tela cortada en forma de polígono regular. Calcula la cantidad de tela que necesitará para fabricar 36 sombrillas de 10 lados si sabemos que el lado mide 173 cm y su apotema mide 266,21 cm.
Área bajo la curva: desarrollo, actividad 2
El cálculo de áreas es una de las aplicaciones básicas de las matemáticas. Todas las grandes civilizaciones antiguas desarrollaron métodos sencillos para calcular el área encerrada por líneas poligonales, pero el problema se encontró al tratar de medir el área encerrada por líneas curvas. Este problema no se resolvió hasta finales del siglo XVII con el descubrimiento del cálculo integral. En la primera parte de este tema definiremos el concepto de área bajo una curva, aproximando el área por medio de rectángulos, seguido de un proceso de paso al límite. A continuación, veremos cómo el teorema fundamental del cálculo nos permite calcular el área bajo la curva mediante el cálculo de primitivas. Esto nos llevará a la segunda parte del tema, donde estudiaremos los métodos básicos de integración. En la tercera parte aplicaremos el cálculo integral a la resolución de los problemas básicos: cálculo de áreas, volúmenes, superficies y longitudes de curvas.
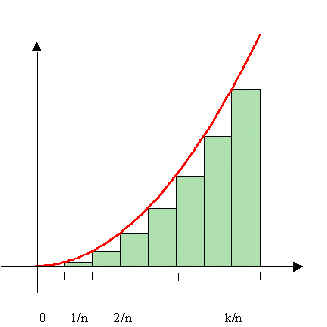
Resuelve el siguiente ejercicio con los conocimientos adquiridos hasta el momento.
Intentará obtener el área formada por la función f(x)=x^2, el eje “x” y el intervalo [-2,2] utilizando algún método conocido o utilizado en sus materias de matemáticas previas al calculo. Comentará los resultados obtenidos, si logró o no calcular el área del ejercicio.