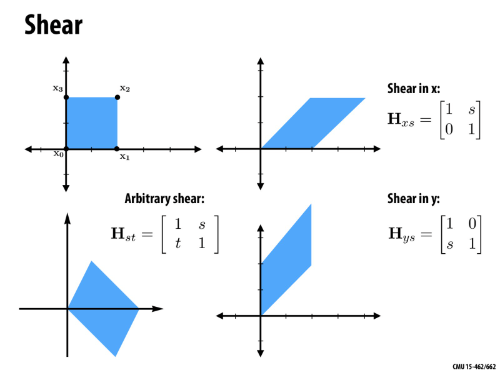
Shearing and Determinants
Shearing Defined
Definition: Shearing is a transformation where a shape is distorted by pushing points in one direction along a line, proportional to their distance from that line, while maintaining the area of the shape.
Matrix Representation of Shearing
We want the shear to either change only the x coordinate and or y coordinate without scaling the shape.
- The diagonal entries remain 1 to ensure no scaling occurs.
- The off-diagonal entries introduce the proportional shift in one coordinate based on the other.
- The zero entries prevent unwanted changes in the other coordinate.
The Unit Square as Reference
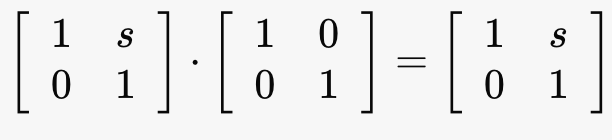
Transforming an arbitrary vector
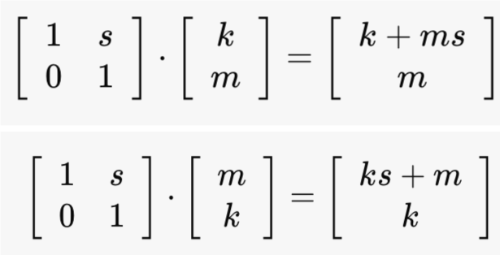
Area of the Transformed Parallelogram
The area formed by the vectors is given by base times height where the base = (length of one side) and the height = (perpendicular distance) where theta is the angle between vectors u and v. Thus, the area = .

This simplifies to |ad-bc| which is the determinant of the matrix formed by the sides of the parallelogram. Thus, the area of the parallelogram is the determinant of the matrix formed by the sides of the parallelogram. When we take the ratio of the new area to the area of the shape before shearing, (determinant of new matrix to original matrix), it will always be 1 indicating that the area doesn't change