Transformando polígonos
![[size=100]A partir de una imagen como puede ser una ventana de cualquier edificio, trataremos de transformarla en otra forma poligonal de manera que se mantenga el perímetro o el área.
Este proceso servirá para describir nuevas transformaciones entre distintos polígonos de manera que mantengan algunas características anteriores o para obtener el mismo polígono
con un área que sea el doble, el triple, etc., del polígono inicial.
Procesos sencillos que se mostrarán de forma gráfica aprovechando las posibilidades que GeoGebra ofrece.[/size]](https://beta.geogebra.org/resource/bsbsh6jz/T4FBqnzxpTaG0YQM/material-bsbsh6jz.png)



Propuesta inicial
Deseamos transformar la ventana rectangular en dos ventanas cuadradas, de manera que:
a. En una se mantenga el área.
b. En otra se mantenga el perímetro.
Rectángulo a cuadrado

De rectángulo a cuadrado

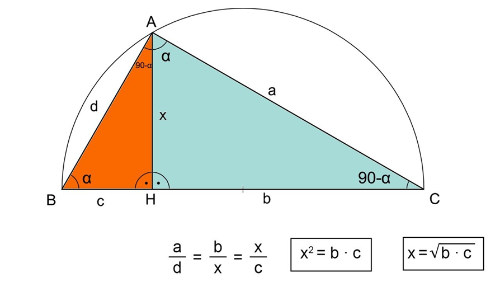
Media aritmética y media geométrica
Teorema de la altura
Ampliando el cuadrado
A partir de un cuadrado ABCD, construye un nuevo cuadrado cuya área sea el doble del área del cuadrado inicial.

Más cuadrados
¿Cómo se podrá construir un cuadrado de área el triple, el cuádruple, …, del área de un cuadrado inicial?
Cuadrado de triple área
Otros polígonos
De rectángulo a triángulo
A partir de un rectángulo, construye un triángulo de igual área.
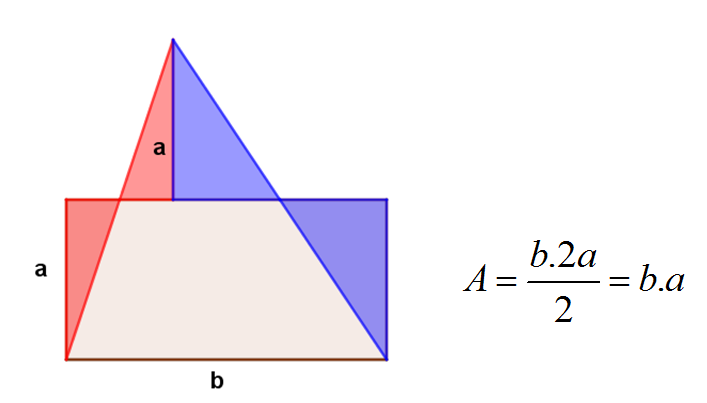
Triángulos de igual área
Sea ABC un triángulo cualquiera.
a. Construye un nuevo triángulo rectángulo cuya área sea igual a la del triángulo ABC.
b. Construye un nuevo triángulo isósceles que tenga igual área que el triángulo inicial.
Triángulos de igual área
Polígonos de igual área
Sea ABCDEF un polígono cualquiera.
Construye un nuevo polígono que tenga un lado menos pero con igual área que el polígono inicial.
Polígonos de igual área
Polígonos de igual área
Piensa cómo construirías un nuevo polígono de igual área, pero con un lado menos.
De hexágono a cuadrado
Paso 1. De hexágono a trapecio
De trapecio a triángulo
De triángulo a rectángulo
De rectángulo a cuadrado
Ventanas circulares

De círculo a cuadrado
Propuesta de actividad
A partir de un cuadrado, construir un círculo cuyo área sea aproximadamente igual a la mitad del área del cuadrado.
