ES 4.5
Given a segment AB, construct a regular pentagon having AB as a side (par = 11, done in 13).
PROCEDURA:
- Traccio una retta passante per due punti A,B qualsiasi.
- Traccio la circonferenza di centro B e raggio AB. Sia E l'altro suo punto di intersezione con la retta AB.
- Traccio la circonferenza di centro A e raggio AB. Siano D,C i suoi punti di intersezione con la circonferenza del punto 2.
- Traccio DC. Sia I il suo punto di intersezione con AB.
- Traccio la circonferenza di centro E e raggio AE.
- Traccio la circonferenza di centro A e raggio AE. Siano F,G i suoi punti di intersezione con la circonferenza del punto 5.
- Traccio FG. Sia H il suo punto di intersezione con la circonferenza del punto 2.
- Traccio la circonferenza di centro I e raggio IH. Sia J il suo punto di intersezione con la retta AB.
- Traccio la circonferenza di centro A e raggio AJ. Siano L, K i suoi punti di intersezione con DC e N quello con la circonferenza del punto 2.
- Traccio AK. Sia O il suo punto di intersezione con la circonferenza del punto 3.
- Traccio OL.
- Tracco LN.
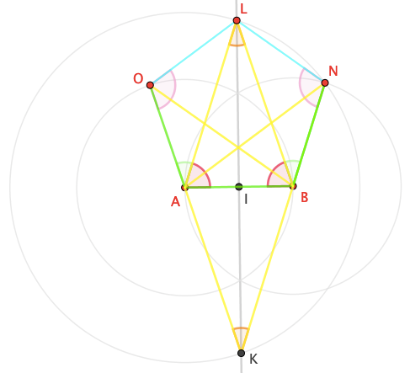
- Traccio NB. ABNLO è il pentagono regolare cercato.
- AOABBN per costruzione (raggi di circonferenze raggio AB).
- △AIL△BIL perchè AIIB (I punto medio per costruzione), IL in comune, angoli LIA e LIB retti per costruzione. In particolare ALBL e gli angoli LAB e LBA sono congruenti (△LAB isoscele).
- △AKI△IKB perchè AIIB, IK in comune, angoli AIK e BIK retti. Inoltre ALAK perchè raggi della stessa circonferenza, quindi si ottiene BLALAKBK e △ABL△ABK per (SSS). In particolare gli angoli AKB e ALB sono congruenti.
- △OKL△LKN perchè OKNK (somma segmenti congruenti), gli angoli OKL e LKN sono congruenti perché △AKI△IKB e LK in comune. In particolare si ottiene che OLLN e che gli angoli KOL e KNL sono congruenti.
- △AOL△LNB per (SSS) e in particolare gli angoli OAL e LBN sono congruenti.
- Gli angoli OAB e ABN sono congruenti per somma di angoli congruenti e quindi △OAB△ABN per (SAS). In particolare OBAN.
- ANAL perchè raggi della stessa circonferenza quindi OBANALLB.
- Consideriamo l'angolo LAN. Esso è un angolo al centro (circonferenza centro A e raggio AL) e un corrispondente angolo alla circonferenza è LKN. Quindi l'angolo LAN è il doppio di LKN. Ma anche l'angolo AKB è il doppio di LKN per quanto dimostrato prima, quindi gli angoli LAN e AKB sono congruenti e inoltre, per i punti precedenti, sono congruenti anche all'angolo ALB.
- △ALB△LAN per (SAS) e in particolare ABLN. Quindi otteniamo che NBOAABLNOL.
- △ABN△LBN per (SSS) e in particolare gli angoli ABN e LNB sono congruenti.
- I triangoli △AOL, △OAB, △ABN, △LBN sono tutti congruenti per (SSS) e isosceli, quindi tutti gli angoli alla base sono congruenti. Ma allora anche l'angolo OLN è congruente all'angolo OAB perchè sono somma di angoli congruenti (ricordando che gli angoli ALB e LAN sono congruenti per quanto detto prima).
- Abbiamo quindi dimostrato che NBOAABLNOL e che gli angoli OAB, ABN, BNL, NLO e LOA sono tutti congruenti, quindi ABNLO è un pentagono regolare.