Indeterminación (límites de funciones)
En esta página explicamos en qué consisten las indeterminaciones que aparecen en los límites, proporcionamos una lista de las mismas y las reglas para operar con infinitos/ceros en las no indeterminaciones. Después, resolvemos algunos límites aplicando las reglas vistas y algunos límites básicos con indeterminaciones.
1. Introducción
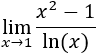En un principio, las funciones del numerador y del denominador están bien definidas para el punto x=1, pero si sustituimos el punto x=1 en ambas, obtenemos la expresión 0/0:
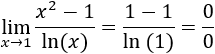Obviamente, este resultado no tiene sentido matemáticamente.
Algo parecido ocurre al calcular el límite siguiente:
Sin embargo, hay una diferencia sustancial entre ambos resultados: podemos asegurar el resultado de todos los límites en los que aparece la expresión 1/0 es ∞, pero no podemos predecir el resultado de los límites en los que aparece 0/0.
Por esta razón, decimos que la expresión 0/0 es una indeterminación. Cuando aparece una indeterminación en un límite, el límite depende de la propia función. Esto conlleva que, aunque aparezca la misma indeterminación, el límite puede ser distinto para funciones distintas.
2. Lista de indeterminaciones
Existen otras expresiones similares a las anteriores pero que no son indeterminaciones, puesto que tenemos reglas que proporcionan el resultado.3. Reglas
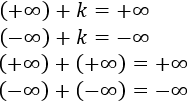2. Productos con infinito:
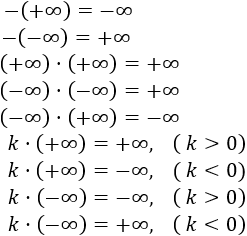3. Cocientes con infinito ó 0:
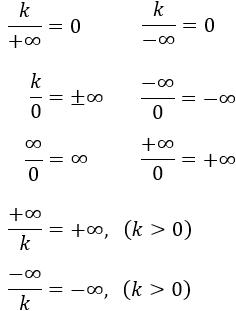4. Potencias con infinito:
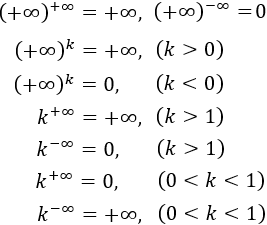
4. Ejemplos
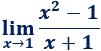Solución:
Al sustituir x por 1, obtenemos el resultado 0/2, así que el límite es 0:
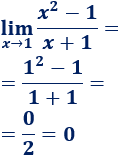Límite 2
Solución:
Sustituimos el punto:
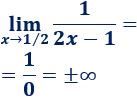Hemos escrito el signo ± porque el signo del límite depende del lado por el que nos aproximamos al punto.
Si nos aproximamos por la derecha, el denominador es positivo y se aproxima a 0, así que el límite es +∞; por el otro lado, el límite es -∞:
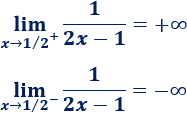Como los límites laterales no coinciden, no existe el límite.
Límite 3
Solución:
Tenemos la indeterminación infinito menos infinito. Sin embargo, como la función exponencial crece mucho más rápido que la función logaritmo, la función siempre es negativa (para x grandes) y, además, cada vez es más negativa. Por tanto,
Límite 4
Solución:
En el denominador tenemos una resta de infinitos. Podemos dividir el numerador y el denominador por la exponencial de mayor base, operación que no cambia la función:
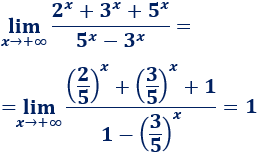Al dividir entre la exponencial, tenemos exponenciales cuya base está entre 0 y 1, así que tienden a 0 cuando x tiende a infinito positivo.