Perpendicular Bisectors and the Circumcenter
What is a perpendicular line?
What does the word "bisector" mean?
Creating a Perpendicular Bisector
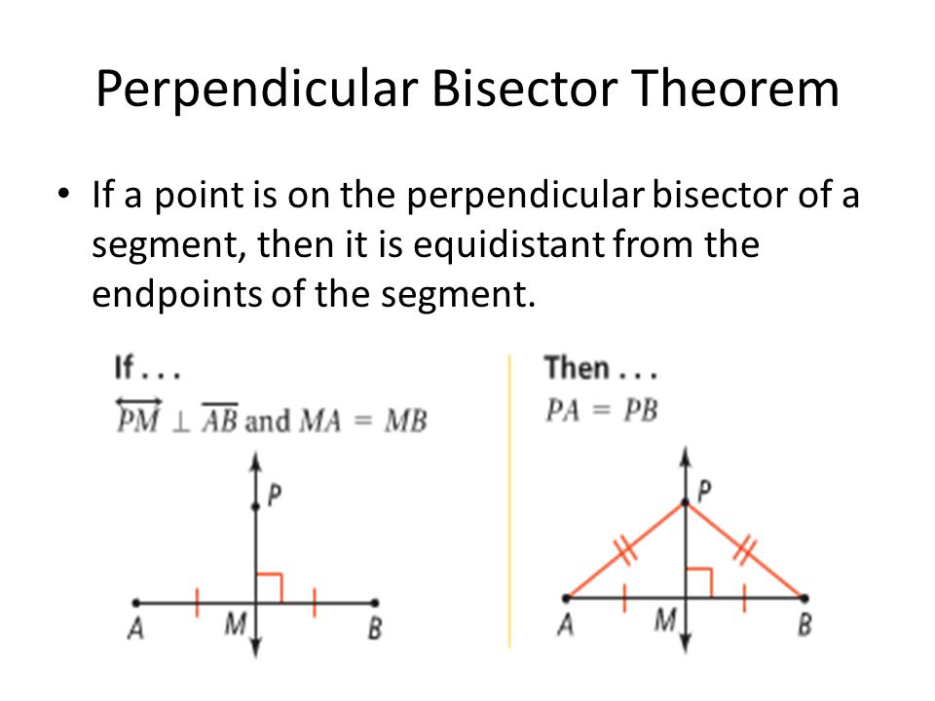
What is the relationship between the distance of the point on the perpendicular bisector to the endpoints of the original segment?
What happens to the angles and side lengths you have if you click and drag point D?
What happens to the angles and side lengths you have if you click and drag one of the end points?
IN YOUR NOTES: Please copy your ending drawing from the Geogebra applet and this theorem to your notebook paper.
Along with in class instructions create a triangle and the perpendicular bisector of the side.
Study the triangle's 3 perpendicular bisectors carefully. As you change the size and shape of the triangle, study how these intersect.
Describe how these three lines meet.
Circumcenter
Is it possible to drag the vertices of the triangle around so point K lies anywhere outside the triangle? If it is possible, describe the type of triangle this occurs with.
Is it possible to drag the vertices around so point K lies anywhere ON the triangle? If possible, describe the type of triangle that this occurs in.
Is it possible to drag the vertices around so point K lies anywhere INSIDE the triangle? If possible, describe the type of triangle that this occurs in.
Go back to the Geogebra applet. Create line segments from the circumcenter to each vertices. Measure the distance of each of these segments.
What do you notice about these distances as you click and drag the vertices of the triangle around?
Using the circumcenter as the center, create a circle that passes through one of the vertices.
What do you notice about this circle? Be specific.