"Cycloid" with variable radius
The cycloid is the locus of a point on a circumference (with a constant radius) that rolls on a straight line. But what if we vary its radius along the way?
This applet allows you to visualize the trace formed by varying the radius according to the angle (in radians) of rotation of the circumference. Negative values for the radius are understood as a circumference below the x-axis rotating to the left (test it!).
A cool fact is that the area under a cycloid period is exactly 3 times the area of the circle that generated it. When we vary the radius, on the other hand, it does not make sense to think of the "area under a period" because the trace is not always (almost never, in fact) periodic. This leads us to the following question: for what functions is the trace such that we can divide it at similar (not necessarily equal) intervals?
To make the job easier, we will place two more restrictions:
(1) traces of consecutive intervals are proportional by a constant factor - this allows you to calculate the area of any interval knowing the area of the first;
(2) corresponding points at different intervals are associated with the same angle in relation to the vertical axis (figure 1).
Figure 1
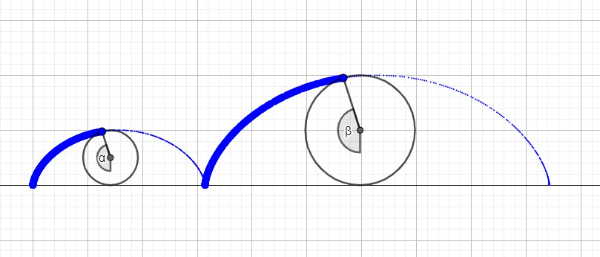
Figure 2
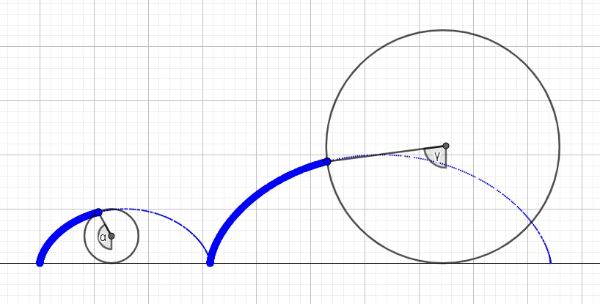
With both constraints, we know that the radius at two corresponding points of consecutive intervals are proportional for the same ratio , that is, . Some solutions to this equation are:
(1) for a constant. In this case, and the generated trace is the cycloid;
(2) and, in this case, ;
(3) or any combination of sinusoid. In this case, ;
(4) or any combination of sinusoid. In this case, .
As you can see, the case corresponds to the periodic functions and there are a multitude of solutions other than those presented.
Obs:
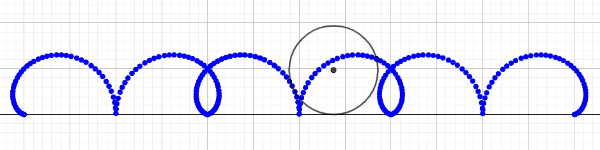
(1) the solution (3) generates a well-known trace;
(2) the solution (4) doesn't repeat periodically in this applet because Geogebra doesn't seem to be able to calculate the right value of the integral of the sine module for points outside the range . Fixing this (manually), the result is the one shown in figure 3.
Figure 3
Finally, for those interested in building this applet, note that the coordinates of the center of the circumference in relation to the angle of rotation are (in fact, the product between the angle in radians and the radius of the circumference results in the arc traversed for a constant radius: generalizing, we have that the integral of the radius in relation to the angle results exactly in the horizontal displacement of the center of the circumference). In addition, the coordinates of the point traced over the circumference are given by (the last term is the versor that gives the direction of the point in relation to the center of the circle).