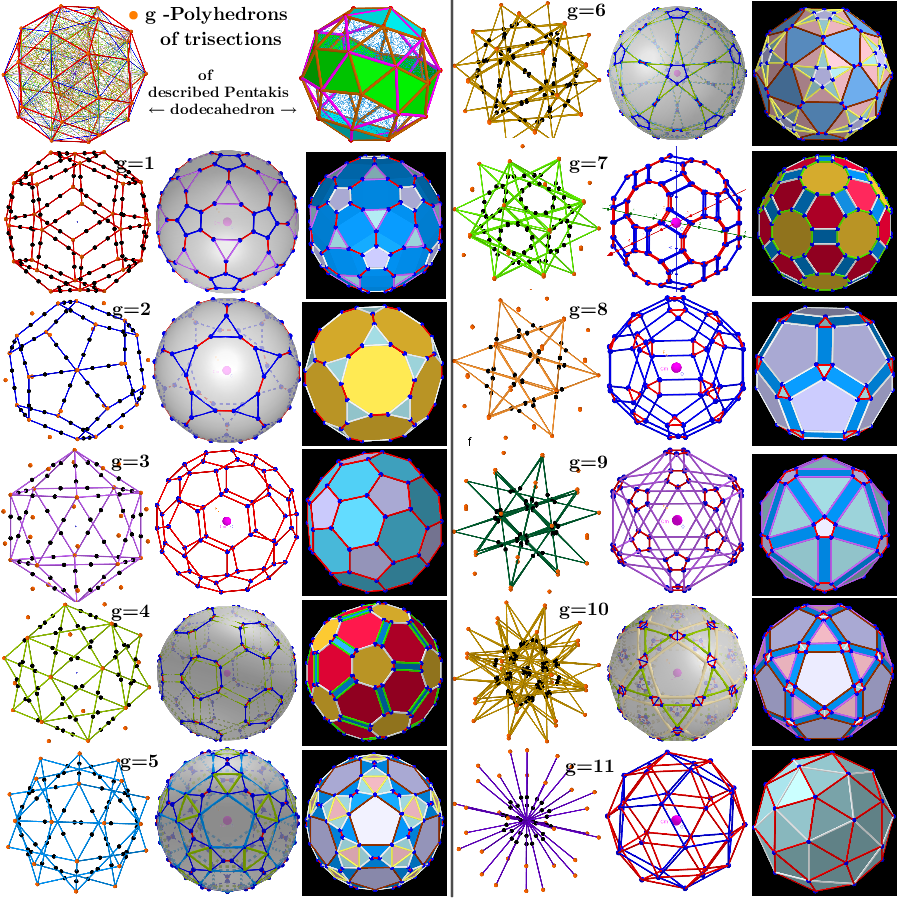
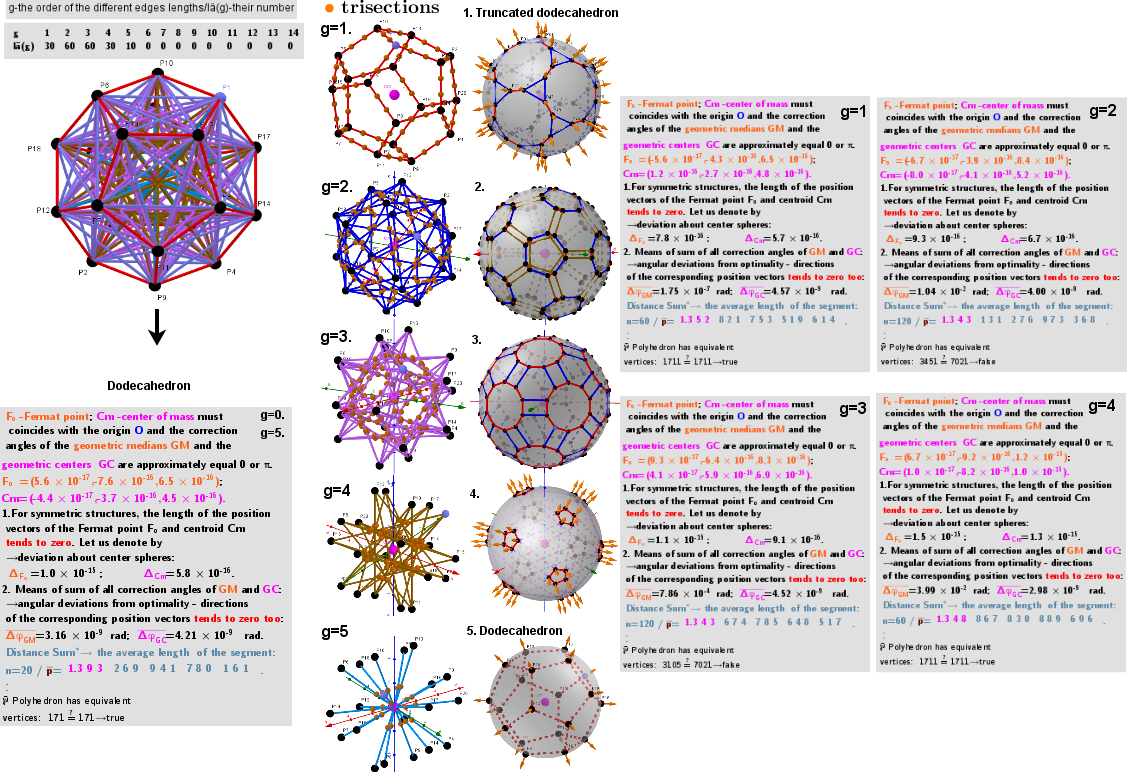
Images. Series of polyhedra obtained by trisection (truncation) different segments of the original polyhedron

Author:: Roman Chijner

Topic:: Algebra, Calculus, Circle, Difference and Slope, Differential Calculus, Differential Equation, Optimization Problems, Geometry, Function Graph, Intersection, Linear Programming or Linear Optimization, Mathematics, Sphere, Surface, Vectors

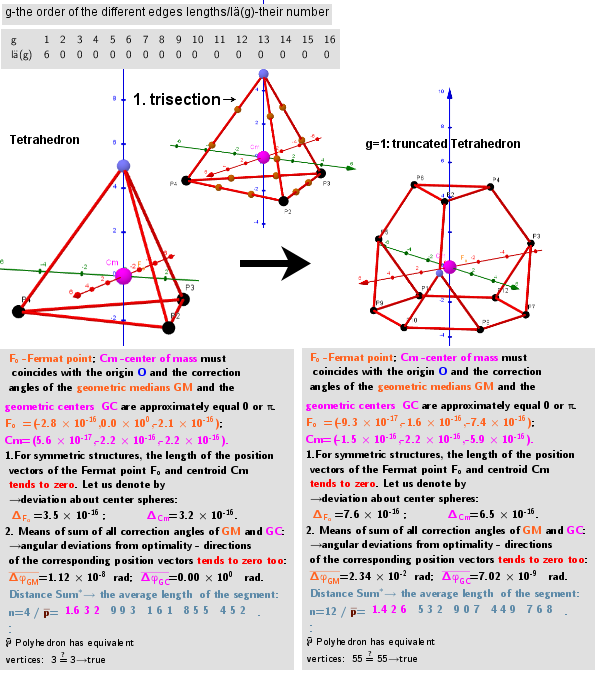
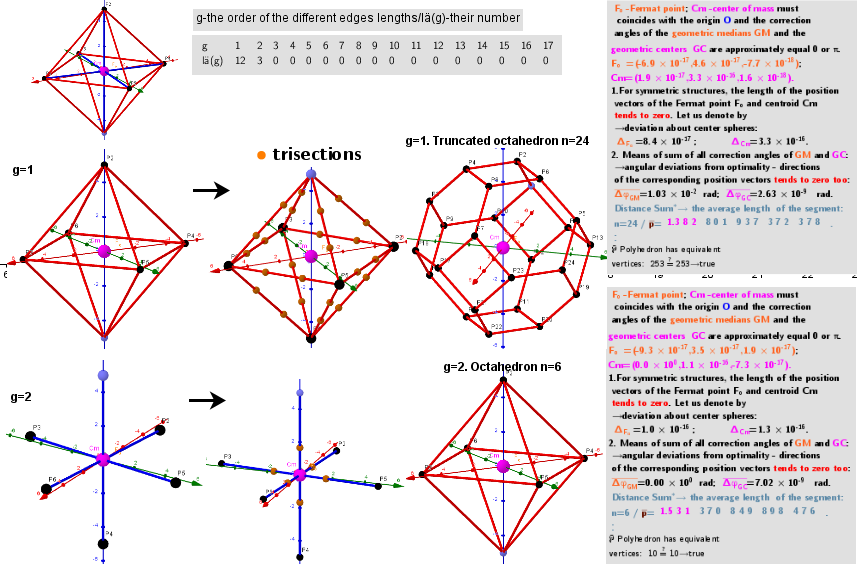
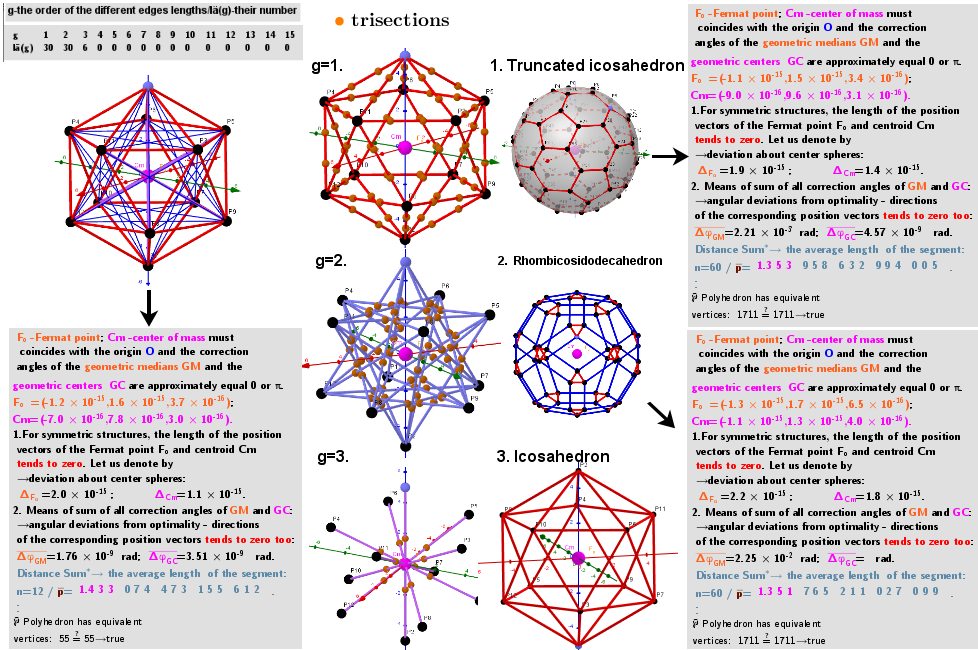
Let the vertices of the initial polyhedron belong to the same sphere. On its basis, can be constructed a certain series of polyhedra. The vertices of each of them are the points of the trisections of the segments of the original polyhedron that have the same length (calculated with a certain accuracy). Obviously, the number of vertices of the constructed polyhedron is twice the number of trisected segments and they all lie on the same sphere. Let g be the ordinal number of the various segments of the initial polyhedron. Geometric Constructions are in Applet.

Series of polyhedra obtained by trisection (truncation) different segments of the original polyhedron- Tetrahedron

Series of polyhedra obtained by trisection (truncation) different segments of the original polyhedron- Octahedron

Series of polyhedra obtained by trisection (truncation) different segments of the original polyhedron- Cube

Series of polyhedra obtained by trisection (truncation) different segments of the original polyhedron- Icosahedron

Series of polyhedra obtained by trisection (truncation) different segments of the original polyhedron- Dodecahedron

Series of polyhedra obtained by trisection (truncation) different segments of the original polyhedron- Biscribed Pentakis Dodecahedron

* From Applet: Serie of polyhedra obtained by trisection (truncation) segments of the Biscribed Pentakis Dodecahedron