Schülerthema Eigenschaften Höhenschnittpunkt
Dieses dynamische Arbeitsblatt ermöglicht eine Musterlösung des Arbeitsblattes, durch welches die Schülerinnen und Schüler an die Eigenschaften des Höhenschnittpunktes herangeführt werden sollen.
Durch die Kontrollkästchen und die Erläuterungen können die einzelnen Schritte nachvollzogen werden.
Vorgehensweise Aufgabe 1
1. Klicke auf das erste Kontrollkästchen (Schritt 1: Erstellen eines Dreieckes), um ein Dreieck zu konstruieren.
Die Schülerinnen und Schüler könnten dieses Dreieck mit dem Werkzeug "Vielecke > Vieleck" erstellen.
2. Klicke auf das zweite Kontrollkästchen (Schritt 2: Einzeichnen der Höhengeraden), um die (verlängerten) Höhen des Dreiecks einzuzeichnen.
Die Schülerinnen und Schüler könnten die Höhengeraden mit dem Werkzeug "Konstruieren > Senkrechte
Gerade" einzeichen, indem sie zunächst auf einen Eckpunkt des Dreiecks und danach auf die
gegenüberliegende Linie klicken. Wichtig dabei ist, dass die Unterscheidung zwischen der Höhe und der
Höhengerade den Schülern deutlich gemacht wird. Um den Höhenschnittpunkt bei jedem Dreieck
einzeichnen zu können, ist es sinnvoll mit Höhengeraden umzugehen. Dies entspricht "verlängerten
Höhen".
Um die Grafik übersichtlich zu gestalten ist es immer sinnvoll, wenn die Schülerinnen und Schüler die
Geraden richtig beschriften und eventuell farblich hervorheben.
3. Klicke auf das dritte Kontrollkästchen (Schritt 3: Einzeichnen des Höhenschnittpunktes), um den Schnittpunkt der Höhengeraden einzuzeichnen.
Die Schülerinnen und Schüler könnten den Schnittpunkt mit dem Werkzeug "Punkte > Schneide" erstellen.
Auch hier ist es empfehlenswert, wenn die Schülerinnen und Schüler diesen Punkt in "H" umbenennen,
damit diese von vorne herein die korrekte Bezeichnung erlernen.
Es sind auch andere Werkzeuge möglich, um die Aufgabe zu lösen. Die vorgeschlagenen Vorgehensweisen ist als mögliche Musterlösung anzusehen.
Die Schülerinnen und Schüler sollen anschließend die Eckpunkte des Dreiecks verschieben und sehen, dass sich auch die Lage des Höhenschnittpunktes verändert. Auf diese entdeckte Erkenntnis baut Aufgabe 2 des Arbeitsblattes auf.
Anhand der GeoGebra-Datei lässt sich durch den Schieberegler "Alpha" der Wert des Winkels α verändern. Hier erkennt man gut, was mit dem Höhenschnittpunkt H passiert, wenn sich die Winkel eines Dreiecks verändern. Dies ist für die nachfolgende Aufgabe, bei der es um den Höhenschnittpunkt bei stumpf-, spitz- und rechtwinkligen Dreiecken geht, besonders wichtig.
Die Schülerinnen und Schüler sollen dies anhand ihrer Konstruktion auch herausfinden, allerdings ist es für Schüler der angesprochenen Klassenstufe leichter, dies durch verschieben der Punkte des Dreiecks herauszufinden statt einen Schieberegler einzubauen, da sonst auch die Konstruktion des Dreiecks anders erfolgen muss.
Zur Verdeutlichung:
Spitzwinkliges Dreieck: 34°< Alpha < 90°
Stumpfwinkliges Dreieck: Alpha < 34° v Alpha > 90°
Rechwinkliges Dreieck: Alpha = 34° v Alpha = 90°
Hinweis: Es sollte allerdings darauf geachtet werden, dass die Schüler sich die Werte der Winkel anzeigen lassen, da diese für die Bearbeitung der zweiten Aufgabe wichtig ist. Näheres hierzu ist in der Vorgehensweise zu Aufgabe 2 beschrieben (s. u.)
Vorgehensweise Aufgabe 2
1. Klicke auf das vierte Kontrollkästchen, um die Winkel des Dreiecks anzeigen zu lassen.
Die Schülerinnen und Schüler könnten die Winkel mit dem Werkzeug "Messen > Winkel" einzeichnen
lassen. Hierbei ist wichtig, dass der Innenwinkel konstruiert wird, um es anschaulicher zu machen.
Wichtig hierbei ist, dass die Schüler sich auch die Werte der Winkel anzeigen lassen. Dies ist durch das
Auswählen des jeweiligen Winkel mit der rechten Maustaste unter dem Aspekt Einstellungen >
Grundeinstellungen > Beschriftung durch die Auswahl "Name + Wert" in dem Drop-down-Menü
einstellbar.
In der GeoGebra-Datei ist dies durch ein zusätzliches Textfeld gewährleistet. Dieses erstellt man, indem man durch das Werkzeug "Medien > Text". Hierbei muss zunächst ein Text (bpsw. Winkel α =) eingeben werden und anschließend muss unter "Erweitert > GeoGebra" das Objekt eingefügt werden. Dies gewählleistet, dass in dem Textfeld immer der aktuelle Wert des Winkels beschrieben ist. Die Texte der anderen Winkel werden analog eingefügt.
Die Schülerinnen und Schüler sollen nun die Eckpunkte des Dreiecks so verschieben, dass sie erkennen können, wie sich die Lage des Höhenpunktes in Bezug auf verschiedene Arten eines Dreiecks verändert.
Hierbei ist wichtig, dass sie bereits Vorkenntnisse zu spitz-, stumpf- und rechtwinkligen Dreiecken besitzen. Eventuell müsste dieses Vorwissen erneut aktiviert und vor der Bearbeitung wiederholt werden.
2. Vervollständigung der Sätze auf dem Arbeitsblatt:
1. Bei einem spitzwinkligen Dreieck liegt der Höhenschnittpunkt H innerhalb des Dreieckes.
2. Bei einem stumpfwinkligen Dreieck liegt der Höhenschnittpunkt H außerhalb des Dreieckes.
3. Bei einem rechtwinkligen Dreieck liegt der Höhenschnittpunkt H im Scheitelpunkt des rechten Winkels.
3. Bearbeitung der Aufgabe 2c:
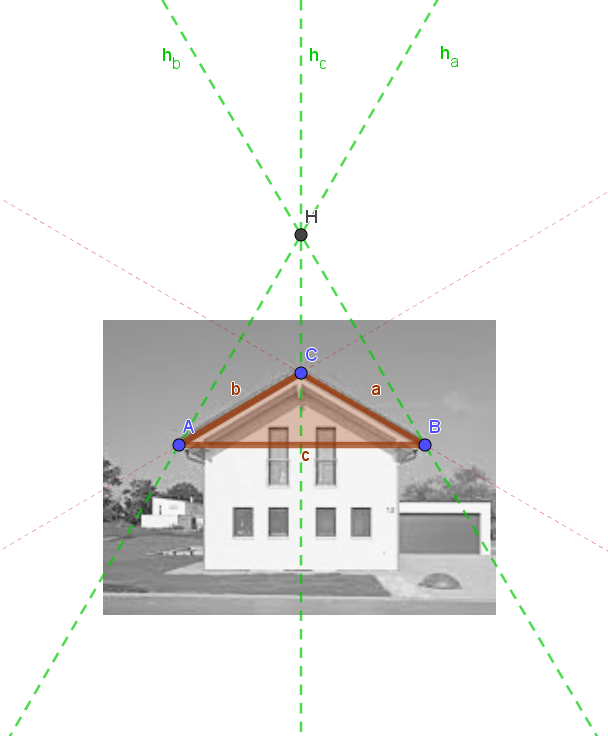
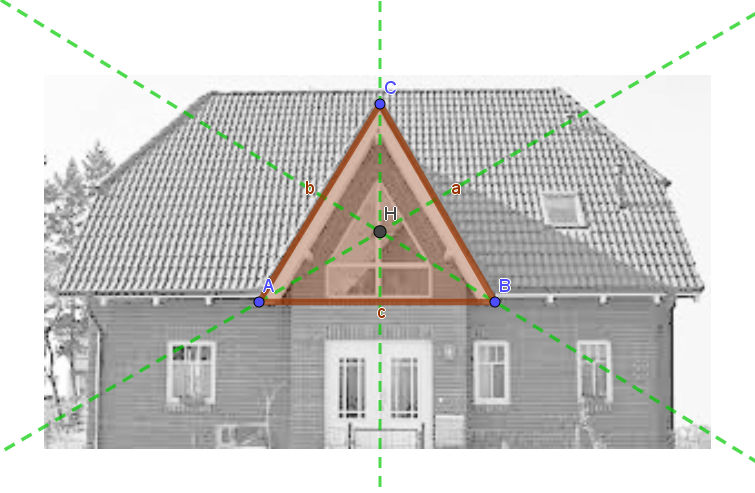
Die Aufgabe 2c soll auf dem Arbeitsblatt selbst bearbeitet werden. Hierzu sollen die Schülerinnen und Schüler die Höhengeraden und den Höhenschnittpunkt der vorgegebenen Dreiecke, die die Dächerform von Häusern abbilden, einzeichnen. Anschließend sollen Antwortsätze formuliert werden.
1. Das Dach hat die Form eines stumpfwinkligen Dreiecks, deshalb liegt der Höhenschnittpunkt
außerhalb des Dreiecks.
2. Das Dach hat die Form eines spitzwinkligen Dreiecks, deshalb liegt der Höhenschnittpunkt innerhalb
des Dreiecks.
Diese Aufgabe ist konzipiert worden, damit die Schüler das Einzeichnen der Höhen(geraden) und des Höhenschnittpunktes auch per Hand erlernen. Außerdem werden durch die Häuser und Dachformen auch Konstruktionen aus ihrem Alltag genutzt. Auch hier ist es notwendig die Verlängerung der Höhen als Gerade mit einzuzeichnen, um den Höhenschnittpunkt einzeichnen zu können.