Kalon moskee - zwik op de oostelijke iwan - gp
Kalon moskee (12e E, herbouwd begin 16e E)
De Kalon moskee in Bukhara is een van de grootste moskeeën in Centraal-Azië. Ze staat tegenover de Mir-i-Arab Madrassa en vormt samen het Po-i-Kaylon geheel.
Gedetailleerde informatie en foto's vind je op orientalarchitecture.com.
De moskee werd gebouwd als Vrijdagmoskee met een capaciteit van 12 000 mensen om de hele mannelijke bevolking van Bukhara te kunnen bevatten.
oostelijke Iwan
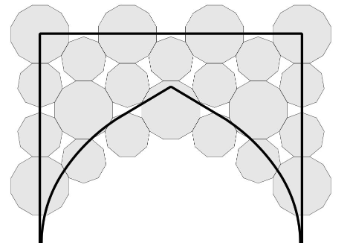
De geometrische decoratie van het zwik van de iwan van de oostelijke hoofdingang combineert 12- en 9-puntige sterren. In onderstaande applet zie je dat deze gegenereerd worden door een vlakvulling met twaalfhoeken, negenhoeken en zeshoekige strikken.
Figuur 1 illustreert dat je met regelmatige twaalf- en negenhoeken samen met strikken inderdaad een regelmatige vlakvulling kunt creëren.
Klassiek construeert men sterfiguren door de middens van zijden van de veelhoeken te verbinden.
- 12-4 ster: - duid in de twaalfhoek het midden van een zijde aan, - tel vier zijden verder en duid het midden van deze zijde aan, - verbind beide punten, - herhaal deze stappen voor de middens van alle zijden, - teken een twaalfpuntige ster.
- 9-3 ster: tel nu telkens drie zijden verder en construeer in een negenhoek een negenpuntige ster.
een vlieger in de strikken
Met de strikken erbij ontstaat er in het lijnenpatroon rond de twaalfhoek een grotere twaalfhoek.
Maar dit lijnenpatroon komt niet helemaal overeen met het patroon op het zwik.
Kijk naar figuur 2: Trek je in een punt van de ster de lijnen door, dan lopen die niet door een ander hoekpunt van de ster, m.a.w. in het echte patroon worden de middens van de zijden van de veelhoeken niet verbonden met het midden van een andere zijde . Waarom niet?
De reden is eenvoudig: in het getekende patroon is een knik nodig is om in de strikken vliegers te bekomen. Daarom wordt de methode om sterren te vormen door middens met middens te verbinden, verlaten zodat doorlopende lijnen in de overgang van veelhoeken naar strikken wel vliegers opleveren.

een 12-4 ster aanpassen
Onderstaand applet toont een 12-4 ster.
Versleep het groene punt. Middens van zijden worden nu verbonden maar met punten ergens tussen het midden van een zijde en het hoekpunt van de twaalfhoek.
Bij het verslepen, merk je dat de tophoeken van de ster verbreden. Het resultaat voor het patroon is dat in het patroon een golvende lijn ontstaat i.p.v. een dominante horizontale lijn en dat zonder een knik doorlopende lijnen in het lijnenpatroon vliegers vormen in de strikken.
Het correcte patroon
De oplossing om met doorgaande lijnen wel een vlieger te bekomen is simpel: keer de logica om.
Vertrek niet van lijnen in de twaalfhoek, maar van de negenhoek en creëer doorlopende lijnen om de tophoek van de twaalfpuntige ster te bepalen.
- Bepaal de middenpunten van de aangrenzende zijden van een twaalfhoek en twee negenhoeken.
- Construeer in de twee negenhoeken een lijn die bij een 9-3 ster hoort.
- Teken de rechten door het middelpunt van de zijde op de twaalfhoek en de middelpunten van de zijden op de negenhoeken en bepaal voor beide rechten het snijpunt met de overeenkomstige vierde zijde in de twaalfhoek.
- Hiermee is de tophoek van de 12-puntige ster bepaald. Je kunt nu in de negenhoeken een 9-3 ster construeren en in de twaalfhoeken een ster met tophoeken zo dat doorlopende lijnen in de strik een vlieger bepalen.