Definizioni e teorema
Definizione: rette incidenti
Due rette incidenti formano quattro angoli, a due a due congruenti perchè sono opposti al vertice.
Se uno dei quattro angoli è retto, tutti i quattro angoli sono retti.

Definizione: rette perpendicolari
Due rette incidenti che formano quattro angoli retti sono perpendicolari.
Si può parlare anche di segmenti perpendicolari, quando appartengono a rette perpendicolari.

Teorema: Esistenza e unicità della perpendicolare
Dati un punto P e una retta r, esiste una e una sola retta passante per P perpendicolare a r.
Ipotesi: P è un punto, r è una retta
Tesi: a) Esiste una retta passante per P perpendicolare a r (dimostrazione dell'esistenza)
b) Questa retta passante per P perpendicolare ad r è unica (dimostrazione dell'unicità)
Dimostrazione - 1° caso: P appartiene ad r
E' una dimostrazione costruttiva:
costruiamo una retta e dimostriamo che è perpendicolare e da questo deduciamo che una retta perpendicolare esiste (perchè l'abbiamo trovata, costruendola).
- P r . Tracciamo una circonferenza (con il compasso) con centro in P e troviamo due punti di intersezione tra la circonferenza e la retta r. Li chiamiamo A e B.
- Puntando il compasso in A e poi in B, tracciamo due archi di circonferenza, aventi lo stesso raggio, che si incontrano un un punto che chiamiamo C.
- Tracciamo la retta PC
Costruzione della retta perpendicolare a r
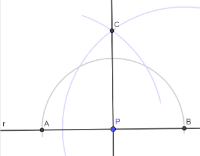
Dimostriamo che la retta costruita è perpendicolare ad r
a) Per costruzione, il triangolo ABC è isoscele, dato che AC BC perchè sono due raggi uguali.
P è il punto medio della base del triangolo ABC e quindi, PC è la mediana.
Ma in un triangolo isoscele, mediana e altezza coincidono. Pertanto, PC è anche altezza del triangolo ABC
e quindi, è perpendicolare alla retta r (che contiene la base del triangolo).
Abbiamo dimostrato che la retta passante per P perpendicolare ad r esiste, perchè ne abbiamo costruita una.
b) Per dimostrare che la perpendicolare è unica, osserviamo che questa retta è la bisettrice dell'angolo
piatto APB e la bisettrice è unica. Pertanto, anche la perpendicolare è unica.
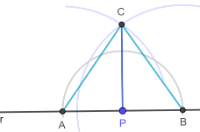
Dimostrazione - 2° caso: P non appartiene ad r
a) Esistenza
- P r . Tracciamo una circonferenza (con il compasso) con centro in P e troviamo due punti di intersezione tra la circonferenza e la retta r. Li chiamiamo A e B.
- Puntando il compasso in A e poi in B, tracciamo due archi di circonferenza, aventi lo stesso raggio, che si incontrano un un punto che chiamiamo C.
- Tracciamo la retta PC.
- Chiamiamo M il punto di intersezione tra r e PC.
- Si formano due triangoli, APC e BPC, che sono congruenti per il 3° criterio, dato che PC è in comune, AP PB perchè sono raggi della stessa circonferenza AC BC perchè sono raggi uguali. Quindi, gli angoli APC e BPC sono congruenti perchè elementi corrispondenti in triangoli congruenti.
- Il triangolo APB è isoscele perchè AP BP.
- PM è la bisettrice dell'angolo al vertice per quanto dimostrato prima. Quindi, dato che il triangolo è isoscele, PM è anche altezza; cioè, è perpendicolare alla base.
- Abbiamo trovato una retta perpendicolare alla base anche in questo caso e quindi, abbiamo dimostrato che una retta perpendicolare ad r esiste anche se il punto P non appartiene alla retta r.
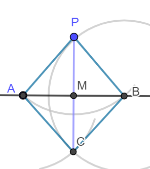
Dimostrazione - 2° caso: P non appartiene ad r
b) Unicità
Si dimostra per assurdo.
Supponiamo che esistano due perpendicolari ad r passanti per P.
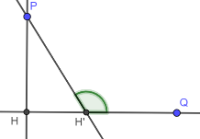
Allora l'angolo PH'Q, che è un angolo esterno per il triangolo PHH', dovrebbe essere maggiore di ciascuno degli angoli interni non adiacenti (per il 1° teorema dell'angolo esterno). In particolare, dovrebbe essere PH'Q > PHH', ma questo è assurdo perchè per ipotesi PHH' e PH'Q sono due angoli retti, dato che sono gli angoli formati dalle due perpendicolari con la retta r. E quindi, sono congruenti.
Pertanto, non possono esistere due rette perpendicolari e quindi, abbiamo dimostrato l'unicità della perpendicolare.