Practice Problems

Here are Circles c and d. Point O is the center of dilation, and the dilation takes Circle c to Circle d.

1. Plot a point on Circle c. Label the point P. Plot where P goes when the dilation is applied.
2. Plot a point on Circle d. Label the point Q. Plot a point that the dilation takes to Q.

Here is triangle ABC.

1. Dilate each vertex of triangle ABC using P as the center of dilation and a scale factor of 2. Draw the triangle connecting the three new points.
2. Dilate each vertex of triangle ABC using P as the center of dilation and a scale factor of 12. Draw the triangle connecting the three new points.
3. Measure the longest side of each of the three triangles. What do you notice?
4. Measure the angles of each triangle. What do you notice? (Question for S2)

Describe a rigid transformation that you could use to show the polygons are congruent.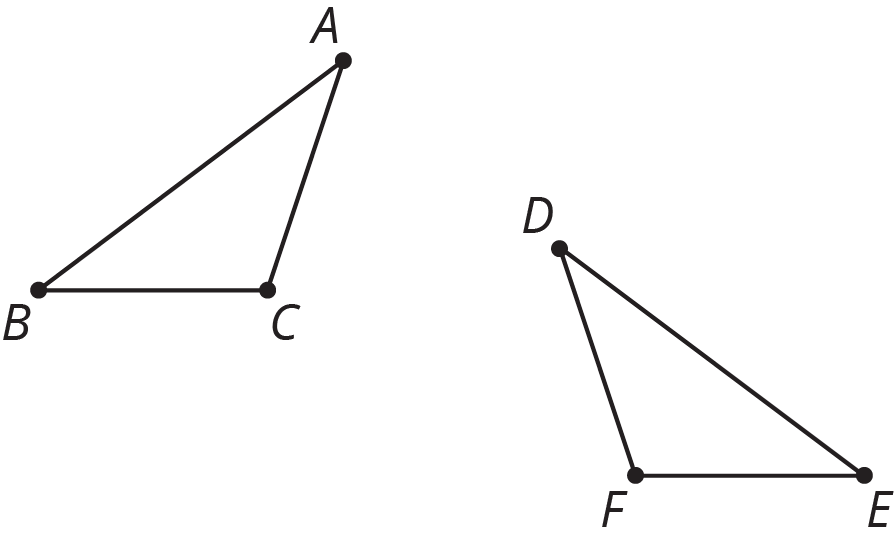

The line has been partitioned into three angles.Is there a triangle with these three angle measures? Explain.

Segment AB measures 3 cm. Point O is the center of dilation. How long is the image of AB after a dilation with . . .

1. Scale factor 5?
2. Scale factor 3.7?
3. Scale factor 15?
4. Scale factor s?

Here are points A and B. Plot the points for each dilation described.

1. C is the image of B using A as the center of dilation and a scale factor of 2.
2. D is the image of A using B as the center of dilation and a scale factor of 2.
3. E is the image of B using A as the center of dilation and a scale factor of 12.
4. F is the image of A using B as the center of dilation and a scale factor of 12.

Make a perspective drawing. Include in your work the center of dilation, the shape you dilate, and the scale factor you use.