Mantelfläche Rotationskörper
In diesem Beispiel möchten wir die Mantelfläche dieser Vase berechnen

Die Form der Vase ist gegeben durch die Rotation der folgenden Funktion um die x-Achse:
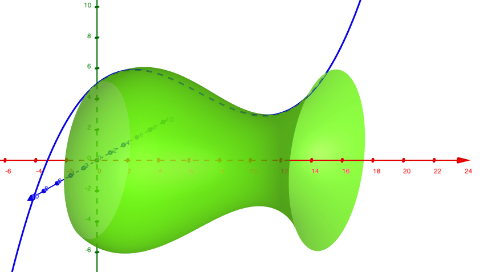
Um die Mantelfläche näherungsweise zu berechnen unterteilen wir die Vase vorerst in Scheiben der Dicke Δx.
Wenn wir die Scheiben genauer betrachten, sehen wir, dass jede Scheibe die Form eines Kegelstumpfes mit der Höhe hat.
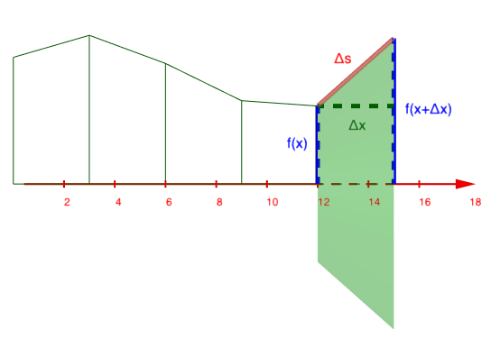
Die Formel für die Mantelfläche eines Kegelstumpfes Lautet . Wobei die Mantellinie des Kegelstumpfes ist.
Die Mantellinie eines jeden Kegelstumpfes in unserer Vase berechnet sich mit dem Pythagoras:
Für jede Scheibe bzw. jeden Kegelstumpf unserer Vase sieht die Formel der Mantelfläche folglich so aus:
Wir verkleinern nun die Höhe dieser Scheiben bzw. Kegelstümpfe um die Form der Vase schrittweise genauer abzubilden.
Für eine unendlich dünne Scheibe lässt sich die Mantellinie berechnen als:
Wir wissen von der Ableitung, dass . Deshalb können wir schreiben
diese Formel führt übrigens zur Bogenlänge, wenn sie integriert wird.
Die Oberfläche dieser unendlich dünnen Scheibe berechnet sich also wie folgt:
und da können wir in der Klammer weglassen.
Mit folgt:
Schliesslich können wir die Mantelfläche berechnen: