Le coniche come luoghi: la parabola
Partendo dalla definizione come luogo geometrico, costruiamo la parabola.
Definizione di parabola.
Assegnati nel piano un punto F e una retta d, si chiama parabola la curva piana luogo geometrico dei punti equidistanti da F e da d.
Cosa significa? Quali costruzioni geometriche possiamo fare per ottenere un punto della parabola?
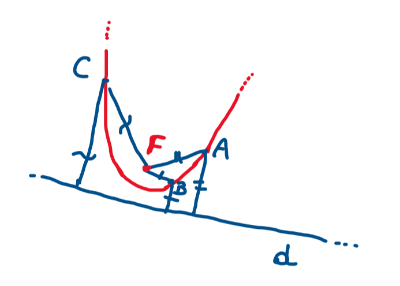
Costruzione:
- Costruisci la retta direttrice d ed il punto F sul piano cartesiano.
- Sia D un punto su tale retta d, costruisci la retta perpendicolare a d passante per D.
- Costruisci l’asse del segmento DF.
- Sia P il punto di intersezione tra queste due rette. Che proprietà soddisfa tale punto?
- Colora di rosso i segmenti congruenti.
- Richiedi la “Traccia attiva” per il punto P.
- Muovi il punto D sulla direttrice.
Per disegnare in modo definitivo la parabola (disabilitare le tracce) scegliere lo strumento “Luogo” e cliccare prima su P (=punto che descrive il luogo geometrico) e poi su D (=punto che genera il luogo geometrico).
Esploriamo i parametri.
Inserisci uno slider per il parametro che varia tra -10 e 10 con incremento 0.1.
Inserisci uno slider per il parametro che varia tra -10 e 10 con incremento 0.1.
Inserisci uno slider per il parametro che varia tra -10 e 10 con incremento 0.1.
Ora inserisci la funzione nella barra di inserimento.
Fai variare i parametri e osserva.