Função Exponencial e Logarítmica
Função Exponencial
Chama-se função exponencial a função tal que em que com .
O número é chamado de base da função.
A função exponencial pode ser crescente ou decrescente a depender do valor da base.
Se função é crescente. Caso contrário é decrescente.
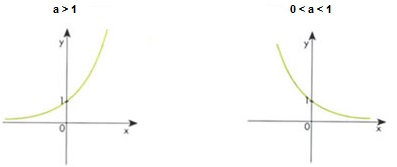
Gráfico da Função Exponencial
Procedimento
Para visualizar a função foi criado um controlo deslizante com valores entre 0 e 10.
De seguida introduz-se a função e visualiza-se o gráfico da função para os vários valores de fazendo deslizar o controlo.
Função Logarítmica
Chama-se função logarítmica à função tal que ,com e . Ao damos o nome de base do logaritmo.
Exemplo:
Esta função é crescente quando e decrescente quando [math]0.
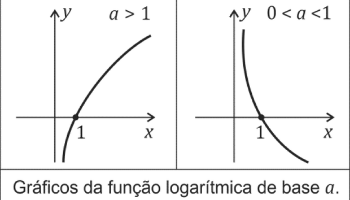
Relação entre as funções
Simetria das funções
Como a função exponencial e logarítmica são inversas, pois , os gráficos das funções são simétricas em relação à reta .
Podemos traçar o gráfico da função logarítmica a partir da exponencial, apresentada a cima, a partir de uma simples simetria.