L6.3 - Types of Transformations
Learning Intentions and Success Criteria
- Compare and contrast (using words and other representations) rigid transformations, similarity transformations, and those that are neither.
- Determine whether a transformation produces congruent or similar images (or neither).
Point B was transformed using the coordinate rule (x, y) → (3x, 3y).
1. Add these auxiliary points and lines to create 2 right triangles: Label the origin P. Plot points M = (2, 0) and N = (6, 0). Draw segments PB’, MB, and NB’. 2. How do triangles PMB and PNB’ compare? How do you know?
3. What must be true about the ratio PB : PB’?
3.2: Congruent, Similar, Neither?
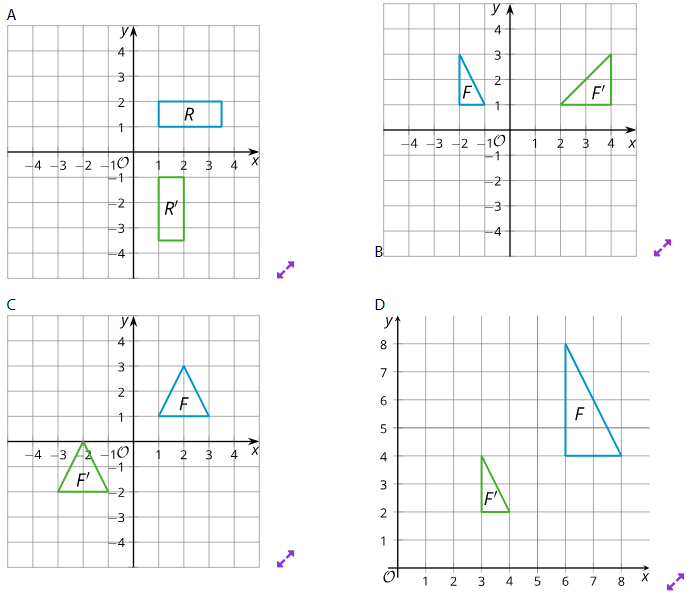
1. (x, y) ()
2. (x, y) (y, -x)
3. (x, y) (-2x, y)
4. (x, y) (x - 4, y - 3)
3.3: You Write the Rules
1. Write a rule that will transform triangle ABC to triangle A’B’C’.
2. Are ABC and A’B’C’ congruent? Similar? Neither? Explain how you know.
3. Write a rule that will transform triangle DEF to triangle D’E’F’.
4. Are DEF and D’E’F’ congruent? Similar? Neither? Explain how you know.
Lesson Synthesis: Types of Transformations
Decide which of the following rules represent rigid transformations, which represent similarity transformations, and which represent neither. 1. (x, y) → (x + 3, y + 1)
2. (x, y) → (x + 12, y - 2)
3. (x, y) → (2x, 2y)
4. (x, y) → (x - 3, y + 8)
5. (x, y) → (2x, 3y)
6. (x, y) → (y, 2x)
7. (x, y) → (,)
8. (x, y) → (-x, y)
9. (x, y) → (-x, -y)
10. (x, y) → (y, -x)
Learning Intentions and Success Criteria
- Compare and contrast (using words and other representations) rigid transformations, similarity transformations, and those that are neither.
- Determine whether a transformation produces congruent or similar images (or neither).
Cool-Down: Write a Rule
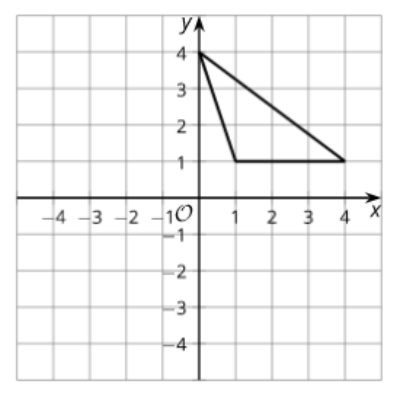
1. Write a rule that will take the triangle to a congruent triangle. You do not need to carry out the transformation.
2. Write a rule that will take the triangle to a figure that is not congruent. You do not need to carry out the transformation.