Un criterio di parallelismo
Teorema: angoli alterni interni e parallelismo
Se due rette tagliate da una trasversale formano una coppia di angoli alterni interni congruenti, allora le rette sono parallele.
Ipotesi:
Tesi: r s
Dimostrazione per assurdo
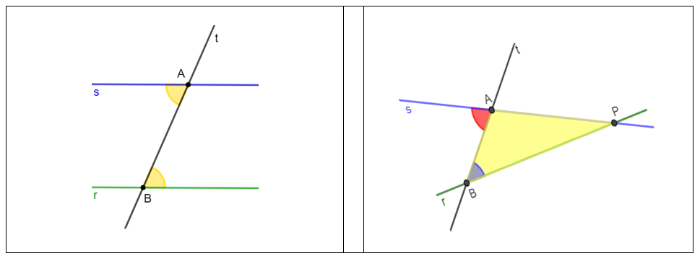
Supponiamo che le rette r ed s non siano parallele. Allora esiste un punto in cui r ed s si incontrano, che chiamiamo P.
Si forma un triangolo APB di cui è un angolo esterno.
Per il primo teorema dell'angolo esterno, (rosso) deve essere maggiore di ciascuno degli angoli interni non adiacenti e quindi, deve essere
> (blu) . Ma per ipotesi, ASSURDO.
Abbiamo trovato una contraddizione dovuta al fatto che abbiamo supposto che la tesi fosse falsa. Pertanto, r ed s devono essere parallele.
Teorema inverso
Se due rette sono parallele, allora, tagliate da una trasversale, formano coppie di angoli alterni interni congruenti.
Ipotesi: r s
Tesi:
Dimostrazione per assurdo
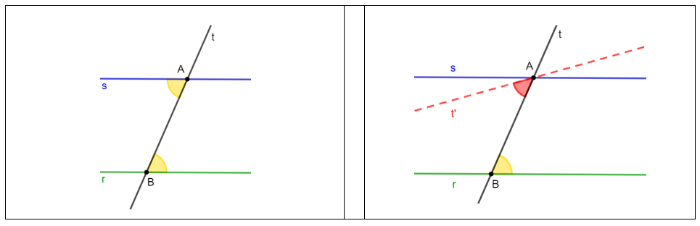
Supponiamo che i due angoli e non siano congruenti. Allora, possiamo tracciare la retta t' passante per A che forma con t un angolo ' .
Ma allora si avrebbe:
- t' r per il criterio di parallelismo perchè t' ed r, tagliate dalla trasversale t, formerebbero una coppia di angoli alterni interni congruenti
- s r per ipotesi.
Questi due teoremi possono essere riassunti in uno solo:
Due rette sono parallele se e solo se, tagliate da una trasversale, formano una coppia di angoli alterni interni congruenti.