Gráficas de las funciones seno y coseno

El seno y el coseno son funciones matemáticas que describen las relaciones entre los lados de un triángulo rectángulo en una circunferencia unitaria (de radio 1).
El coseno se corresponde con la longitud del cateto adyacente (en azul) mientras que el seno lo hace con la del cateto opuesto (en rojo).
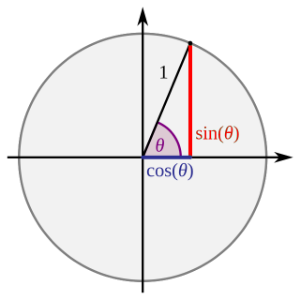
Los valores de los catetos, y por tanto del seno y coseno, dependen del ángulo. En la hoja dinámica se puede ver un círculo unitario con un punto P que se puede mover a lo largo del círculo. El segmento entre el centro de la circunferencia y cualquier punto de ésta define el ángulo θ, y se forma un triángulo rectángulo cuyos catetos son el seno y el coseno del ángulo.
Inicialmente cuando P está en el punto (1,0) el seno vale 0 y el coseno 1, y a medida que se mueve el punto P se visualiza el rastro en la parte derecha de la hoja. Los valores del seno del ángulo se muestran en rojo, mientras que los del coseno del ángulo se muestran en azul.
Actividad 1: Utilizar la hoja dinámica para encontrar los valores de los ángulos cuyo seno es igual a 0, y posteriormente los ángulos cuyo coseno es igual a 0.
Actividad 2: Utilizar la hoja dinámica para comprobar los valores del seno y coseno de π/2 (90°) y de π/4 (45°)
Se puede ver como tanto la función seno como la coseno son periódicas, es decir, se repiten. Se podría decir que se pueden extender copiando y pegando a parte que se repite. Para ambas el periodo es 2π (o 360 grados) ya que al completar una vuelta entera de la circunferencia los valores del seno y coseno se repiten.
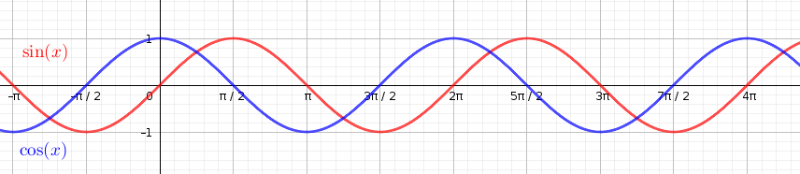
Además, en la imagen anterior se observa como en realidad las funciones seno y coseno son la misma función desplazada.
Desplazando la gráfica de la función coseno π/2 (o 90°) hacia la derecha se obtiene la función seno. Mientras que desplazando la gráfica de la función seno π/2 a la izquierda se obtiene la coseno.
Este desplazamiento se puede obtener cambiando el valor de la fase inicial, que se suele expresar con la letra griega Φ. De manera que para desplazar la función coseno Φ unidades a la derecha se haría:
En la siguiente hoja dinámica se puede ver el efecto de desplazar la función coseno una cantidad Φ, que se puede ajustar moviendo el deslizador. Notar que el valor de la fase inicial viene dado en grados.
Actividad 3: Usar la hoja dinámica para conseguir el valor más pequeño de Φ que haga que la función coseno coincida con la seno. ¿Vuelven a coincidir para algún otro valor de Φ?
Debido sus propiedades, las funciones seno y coseno son muy útiles para modelar fenómenos periódicos, como pueden ser las oscilaciones y ondas.