Iperbole equilatera riferita agli asintoti 1 e funzione omografica
- Autore:
- Federico Chinni, Ilic Ferretti
L'IPERBOLE EQUILATERA RIFERITA AGLI ASINTOTI
In questo paragrafo vediamo un caso particolare di iperbole, molto importante perché rappresenta un caso molto speciale legato alla rappresentazione di grandezze inversamente proporzionali. Introduciamo l'argomento nella seguente animazione.
Da notare che in questo caso particolare l'iperbole è rappresentata da una funzione, dato che ad ogni in input corrisponde un solo di output; questo può essere reso esplicito riscrivendo l'equazione nella forma:
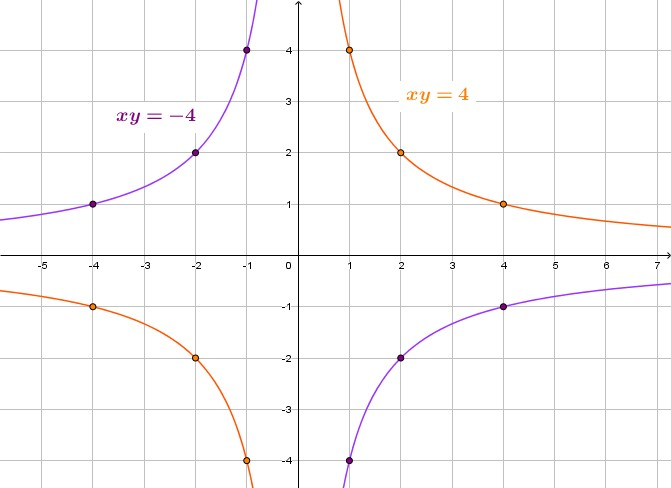
Osserviamo infine che può essere positivo o negativo. Nel primo caso la funzione occuperà il primo e terzo quadrante ( è positivo e quindi è il prodotto di numeri concordi) , altrimenti occuperà il secondo ed il quarto (dove ed sono numeri discordi ed il loro prodotto è negativo).
LA FUNZIONE OMOGRAFICA
Un'iperbole riferita agli asintoti traslata in un nuovo centro qualsiasi viene detta funzione omografica. Ricaviamone l'equazione nell'animazione qui sotto.
Abbiamo visto che la forma generale della funzione omografica è del tipo
con C (-d/c; a/c) centro di simmetria ed equazioni degli asintoti x =-d/c e y = a/c.
dove sono quattro numeri qualsiasi. Vediamo ora come riuscire a dedurre le caratteristiche del grafico di una funzione omografica partendo dai suoi quattro parametri. Osserviamo ad esempio il grafico della funzione , riportata qui sotto.