Spider and fly
A different kind of extreme value task
The following question goes back to Henry Ernest Dudeney (1857 - 1930).
In a room that is 6 m long, 2.40 m wide and 2.40 m high there is a spider and a fly. The spider is in the middle of the front side surface 20 cm above the floor and the fly on the opposite wall is also in the middle but 20 cm below the ceiling.
Which path does the spider have to take along the walls so that it can reach the spider by the shortest possible route?
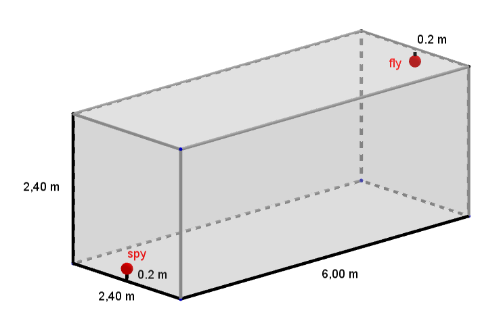
The solution to the task
There are two paths, each 8 m long.
Task
Change the position of the spider on the front side wall of the room and the position of the fly on the back wall and observe the shortest paths in each case.
To solve the extreme value problem
The shortest path can be found by looking at the net of the cuboid space. Here the shortest path can be drawn as a straight line connection between spider and fly. However, there are several options - depending on how the net is designed.
The shortest path is shown in red in the applet.
Notice
In addition to the routes drawn in black, there are other paths (drawn here in yellow) that the spider could take, but for reasons of symmetry they are the same length as other paths.
A very good article on this topic can be found in the online edition of the magazine Spektrum der Wissenschaft https://www.spektrum.de/raetsel/fliege-und-spinne/1797209