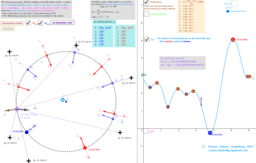
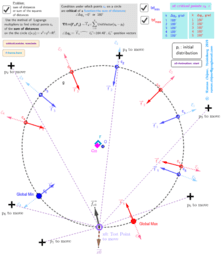
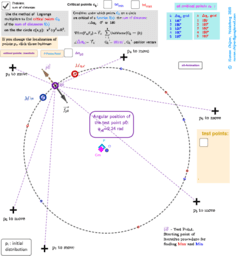
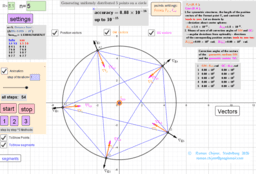
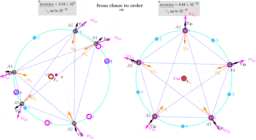
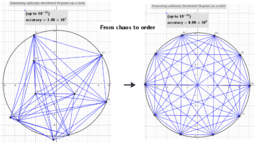
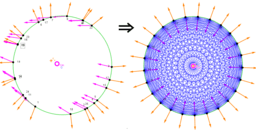
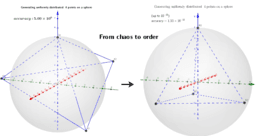
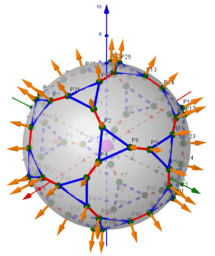
₃Point estimators of location on a circle for a points set

Szerző:Roman Chijner

Témák:2D vektorok (két dimenziós), 3D vektorok (három dimenziós), Algebra, Kör, Differenciálszámítás, Függvények, Geometria, Grafikon, Metszet, Matematika, Felület, Transzformációk, Vektorok

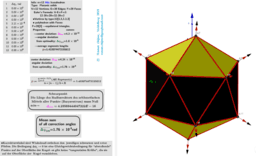
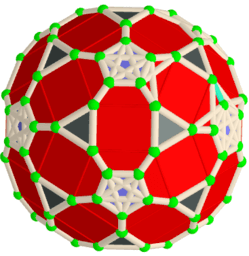
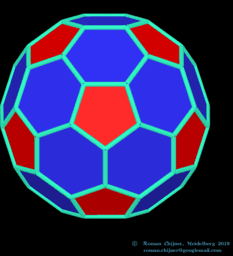
ΛM -Lagrange Multipliers with One Constraint. Finding Estimators of location on a circle or on the surface of the sphere as Critical points of the corresponding Lagrangian for a discrete set of points. From: List of My Public Books on GeoGebra Topics: Constructing polyhedra -https://www.geogebra.org/m/eabstecp