Voorbeeld + opgaven 5 en 6
Voorbeeld 2
Gegeven is de functie f met functievoorschrift f(x) = -5+36x−6x2. Beschrijf het verloop van de grafiek. Bepaal ook de extreme waarde.
Antwoord:
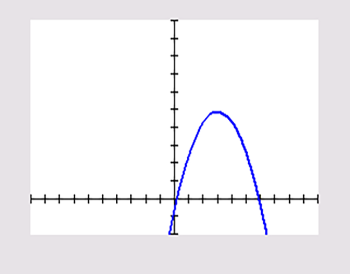
Breng eerst de grafiek goed in beeld, bijvoorbeeld met de grafische rekenmachine. Je berekent dat f een maximum heeft in x = 3. De grafiek is afnemend stijgend op het interval <←,3> en toenemend dalend op <3,→>. Het maximum is f(3)=49.

Opgave 5
Gegeven is de kwadratische functie f met voorschrift f(x) = -x2 + 6x .
a. Plot de grafiek van f en beschrijf de soorten stijging en daling van links naar rechts.
b. Welke extreme waarde heeft deze functie?
Opgave 6
Gegeven is de functie f(x) = x3 −5x.
a. Plot de grafiek van f.
b. Beschrijf de soorten stijging en daling die je in de grafiek ziet. Geef ook de bijbehorende intervallen. Rond indien nodig af op twee decimalen.
c. Geef in twee decimalen nauwkeurig de extreme waarden.