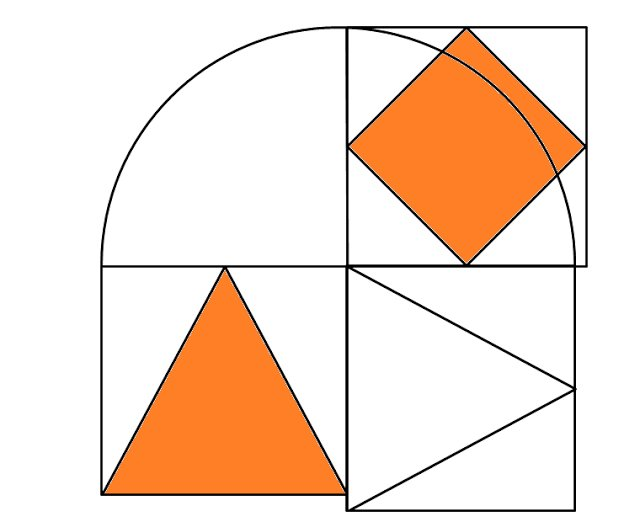
Equivalent square of a equilateral triangle
Following a twitter discussion..
In 1486, Matthias Roriczer presented this method for constructing a square equal in area to a given equilateral triangle. Does it work?
 https://twitter.com/solvemymaths/status/948463424463425536
It turned out that Roriczer's method couldn't work but was just an approximation (rather good).
I then tried to find out an exact solution to the problem of constructing a square equivalent (in area) to a given equilateral triangle. Here is my solution.
https://twitter.com/solvemymaths/status/948463424463425536
It turned out that Roriczer's method couldn't work but was just an approximation (rather good).
I then tried to find out an exact solution to the problem of constructing a square equivalent (in area) to a given equilateral triangle. Here is my solution.
 https://twitter.com/solvemymaths/status/948463424463425536
It turned out that Roriczer's method couldn't work but was just an approximation (rather good).
I then tried to find out an exact solution to the problem of constructing a square equivalent (in area) to a given equilateral triangle. Here is my solution.
https://twitter.com/solvemymaths/status/948463424463425536
It turned out that Roriczer's method couldn't work but was just an approximation (rather good).
I then tried to find out an exact solution to the problem of constructing a square equivalent (in area) to a given equilateral triangle. Here is my solution.
Equivalent square of a equilateral triangle
Improvement
After I had posted above construction @Simon_Gregg twitted an amazingly alternative construction, much more simple and simply beautiful. Here is my Geogebra's reproduction based on his figure.
Simon Gregg's version
Simon Gregg's figure