Circumcenter
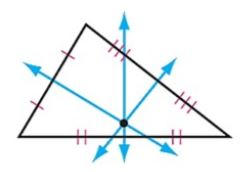
A circumcenter is the point of concurrency of the three perpendicular bisectors.
-Construct triangle XYZ and label the vertices with text tool .
-Construct the perpendicular bisector
.
-Construct the perpendicular bisector  of each side.
-Use the intersect
of each side.
-Use the intersect  in the point menu to mark the circumcenter and name it A with text tool
in the point menu to mark the circumcenter and name it A with text tool  .
.
 .
-Construct the perpendicular bisector
.
-Construct the perpendicular bisector  of each side.
-Use the intersect
of each side.
-Use the intersect  in the point menu to mark the circumcenter and name it A with text tool
in the point menu to mark the circumcenter and name it A with text tool  .
.
Construct the circumcenter below.
Drag the vertices of XYZ around. What kind of triangle is XYZ if the circumcenter A falls on the exterior of the triangle?
What kind of triangle is XYZ if the circumcenter A falls on the triangle?
What kind of triangle is XYZ if the circumcenter A is in the interior of the triangle?
A circumscribed circle (circle that goes through each vertex) can be added in this construction above. Draw a segment from the circumcenter A to vertex X. This creates the radius of the circle (segment AX). Construct a circle on your construction above using your compass tool . Move the triangle around and verify the circle always goes through all vertices X, Y and Z.
. Move the triangle around and verify the circle always goes through all vertices X, Y and Z.
 . Move the triangle around and verify the circle always goes through all vertices X, Y and Z.
. Move the triangle around and verify the circle always goes through all vertices X, Y and Z.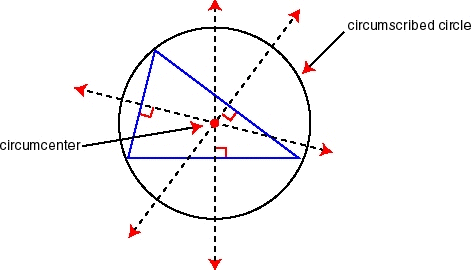
Drag around the vertices of XYZ. Does the circle always go through the three vertices and remain outside the triangle?
Since a circumscribed circle goes through each vertex, the circumcenter is equidistant from each: