S0G3R2 三角形的外角和
引入
这次的 Geogebra 基础课要来实作这个三角形外角和等于一个周角 360° 的动画。
学习指引
这节定位为基础课 Level 2 的难度,因此避免使用指令来作操作。但要实作这个问题,关键还是在于对问题作拆解,对以上动画我作如下拆解:
- 有个三顶点可动的三角形
- 三角形会随着[滑动条]进行缩放
- 标示三角形的外角
- 缩放后,原先三角形的三个控制点隐藏
任务一:作个可缩放的三角形
首先,先建三个点 A,B,C ,接着再建一个滑动条 r 来控制 A,B,C 缩放后的点 rA, rB, rC。再对这三个缩放后的点,连成三角形。此时就可用滑动条控制三角形的缩放。
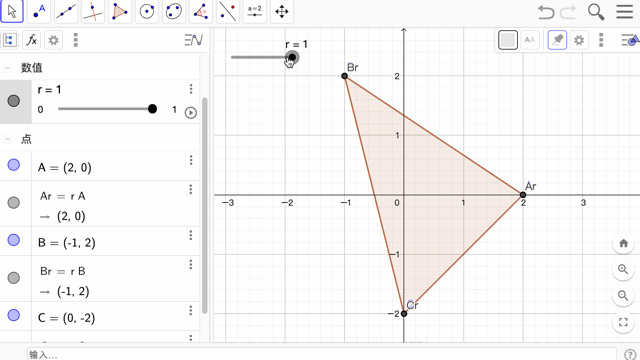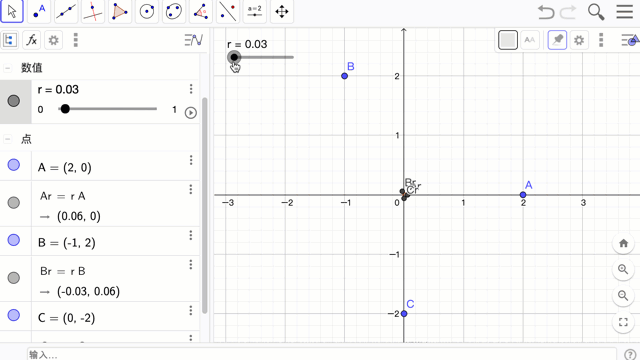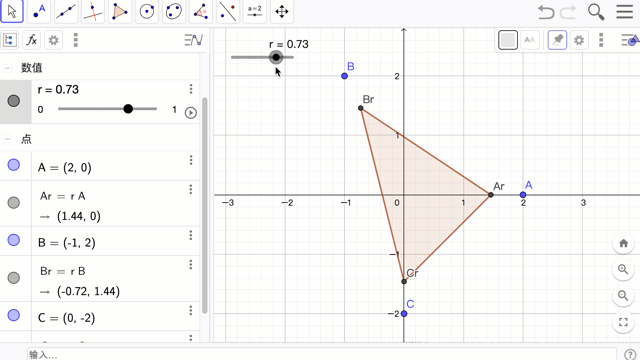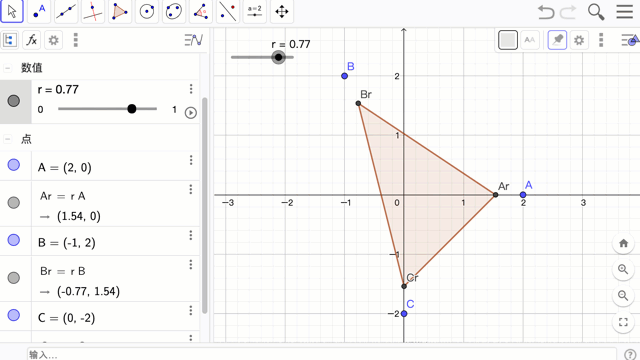
A = (2,0)
B = (-1,2)
C = (0,-2)
r = 滑动条(0,1,0.01,1,100)
Ar = r*A
Br = r*B
Cr = r*B
rABC = 多边形(Ar,Br,Cr)任务二:显示三角形的外角
在这节要绘制外角,让三角形每边的都延伸出一个线段。为了延长一个定长为 1 的线段,我们个别以三角顶点为圆心,绘制一个半径为 1 的圆。接着让每边作个射线取得与圆的交点 D,E,F 。此时再用角度工具就可得到三个外角。
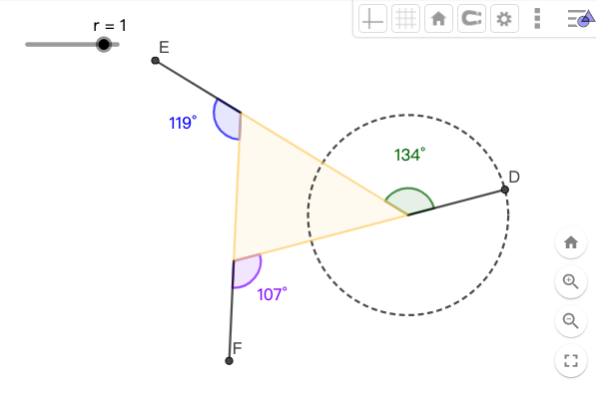
cA = 圆周(Ar,1)
cB = 圆周(Br,1)
cC = 圆周(Cr,1)
D = 交点(cA, 射线(C,A),2)
E = 交点(cB, 射线(A,B),2)
F = 交点(cC, 射线(B,C),2)
aA = 角度(D,Ar,E)
aB = 角度(E,Br,F)
aC = 角度(F,Cr,D)但这时将滑动条缩为 0 时, 角会消失。因此,对滑动条 r 将他的初始值射为 0.001,使得实际上还是要有个三角形,但边长太小而看不见。
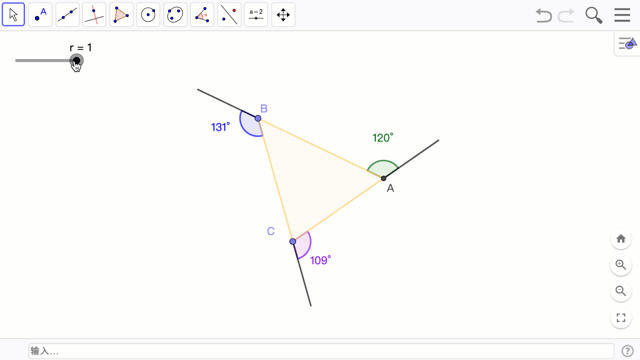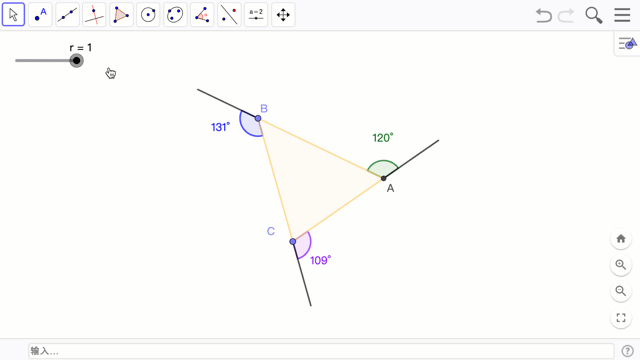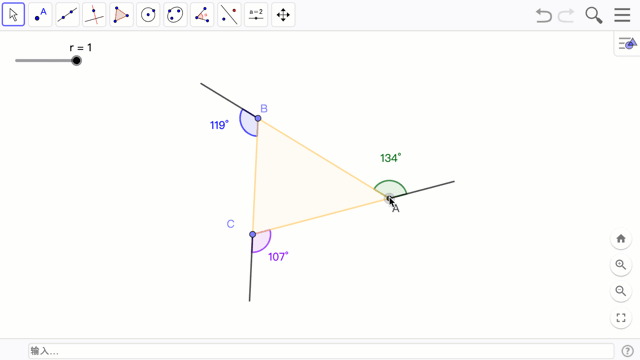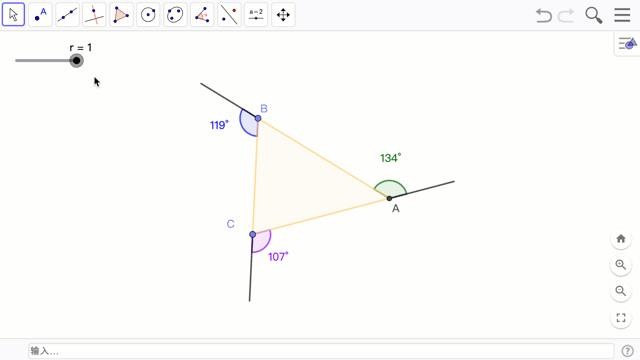
最后还可有些小微调,将 Ar, Br, Cr, D,E,F都隐藏,但对于 A,B,C 可设定为 r=1 才出现,使得回复原状时,可调整三角形的形状。