Rule of Sarrus
To calculate a 3x3 determinant, you need to sum 6 products. Each product is the result of multiplying three elements of the matrix, with the condition that none of the three shares a row or column with another.
 is each instance when a number is greater than another that appears in a later position. For example, the permutation (2 3 1) has two inversions because, when comparing the three numbers in pairs, we see that while 2 < 3, it turns out that 2 > 1 and 3 > 1. The following figure shows the inversions of each permutation.
is each instance when a number is greater than another that appears in a later position. For example, the permutation (2 3 1) has two inversions because, when comparing the three numbers in pairs, we see that while 2 < 3, it turns out that 2 > 1 and 3 > 1. The following figure shows the inversions of each permutation.

 is each instance when a number is greater than another that appears in a later position. For example, the permutation (2 3 1) has two inversions because, when comparing the three numbers in pairs, we see that while 2 < 3, it turns out that 2 > 1 and 3 > 1. The following figure shows the inversions of each permutation.
is each instance when a number is greater than another that appears in a later position. For example, the permutation (2 3 1) has two inversions because, when comparing the three numbers in pairs, we see that while 2 < 3, it turns out that 2 > 1 and 3 > 1. The following figure shows the inversions of each permutation. | = (1 2 3) | |  | = (2 3 1) 2>1 3>1 | |  | = (3 1 2) 3>1 3>2 |
 | = (3 2 1) 3>2 3>1 2>1 | | 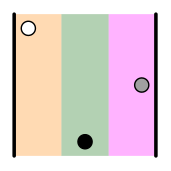 | = (1 3 2) 3>2 | | 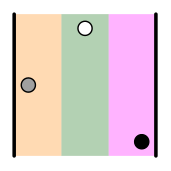 | = (2 1 3) 2>1 |
The first three products have an even number of inversions (0 or 2), while the last three have an odd number (1 or 3). Thus, the first will retain their sign, while the sign of the second will be changed (this is due to Laplace's theorem, i.e., the result of expanding the determinant by a row or a column).
Since it's easy to confuse the permutations, the French mathematician Sarrus  devised a mnemonic rule that now bears his name. It simply consists of adding the first two rows to the end of the matrix (or, alternatively, the first two columns to the right of the matrix) and drawing three diagonals from left to right and three in the opposite direction (these will have their signs changed), as shown in the following construction.
Notice that if you imagine the "bottom edge" of the box containing the determinant coincides with the "top edge," you can mentally move from the bottom to the top without much effort. It’s like when, in a video game, an object disappearing off one side of the screen reappears on the opposite side. This "mental game" is what the upper right part of the construction shows.
Geometrically, by joining two opposite sides of a square (the determinant’s box) without rotating them, we get a cylinder, which is what the lower right part of the construction shows.
As you can see, there are various versions of Sarrus' mnemonic rule. Choose the one you like best!
devised a mnemonic rule that now bears his name. It simply consists of adding the first two rows to the end of the matrix (or, alternatively, the first two columns to the right of the matrix) and drawing three diagonals from left to right and three in the opposite direction (these will have their signs changed), as shown in the following construction.
Notice that if you imagine the "bottom edge" of the box containing the determinant coincides with the "top edge," you can mentally move from the bottom to the top without much effort. It’s like when, in a video game, an object disappearing off one side of the screen reappears on the opposite side. This "mental game" is what the upper right part of the construction shows.
Geometrically, by joining two opposite sides of a square (the determinant’s box) without rotating them, we get a cylinder, which is what the lower right part of the construction shows.
As you can see, there are various versions of Sarrus' mnemonic rule. Choose the one you like best!
 devised a mnemonic rule that now bears his name. It simply consists of adding the first two rows to the end of the matrix (or, alternatively, the first two columns to the right of the matrix) and drawing three diagonals from left to right and three in the opposite direction (these will have their signs changed), as shown in the following construction.
Notice that if you imagine the "bottom edge" of the box containing the determinant coincides with the "top edge," you can mentally move from the bottom to the top without much effort. It’s like when, in a video game, an object disappearing off one side of the screen reappears on the opposite side. This "mental game" is what the upper right part of the construction shows.
Geometrically, by joining two opposite sides of a square (the determinant’s box) without rotating them, we get a cylinder, which is what the lower right part of the construction shows.
As you can see, there are various versions of Sarrus' mnemonic rule. Choose the one you like best!
devised a mnemonic rule that now bears his name. It simply consists of adding the first two rows to the end of the matrix (or, alternatively, the first two columns to the right of the matrix) and drawing three diagonals from left to right and three in the opposite direction (these will have their signs changed), as shown in the following construction.
Notice that if you imagine the "bottom edge" of the box containing the determinant coincides with the "top edge," you can mentally move from the bottom to the top without much effort. It’s like when, in a video game, an object disappearing off one side of the screen reappears on the opposite side. This "mental game" is what the upper right part of the construction shows.
Geometrically, by joining two opposite sides of a square (the determinant’s box) without rotating them, we get a cylinder, which is what the lower right part of the construction shows.
As you can see, there are various versions of Sarrus' mnemonic rule. Choose the one you like best!Author of the construction of GeoGebra: Rafael Losada