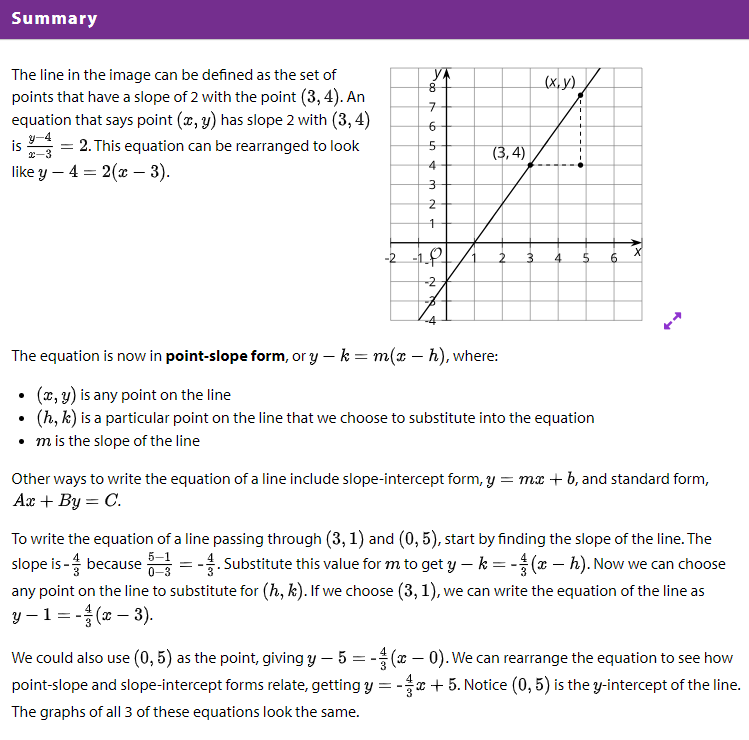
L6.9 - Equations of Lines
Learning Intentions and Success Criteria
- Generalize (using words and other representations) that a line can be represented by an equation in point-slope form.
- Use the definition of slope to write the equation for a line in point-slope form.
9.1: Remembering Slope
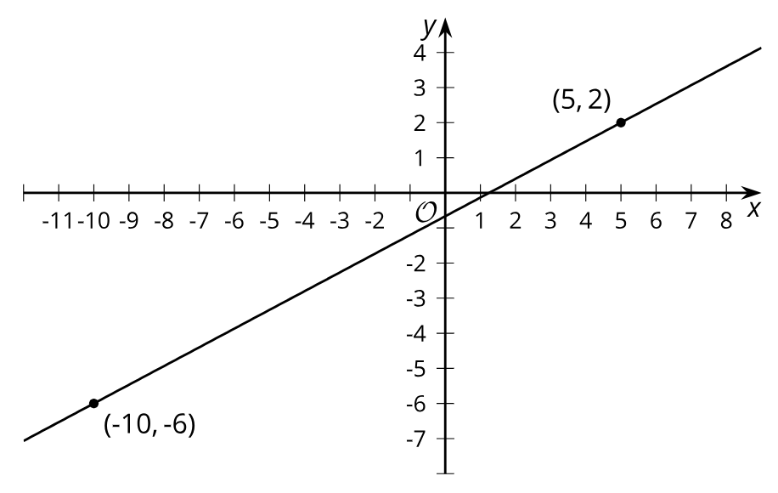
The slope of the line in the image is . Explain how you know this is true.
9.2: Building an Equation for a Line
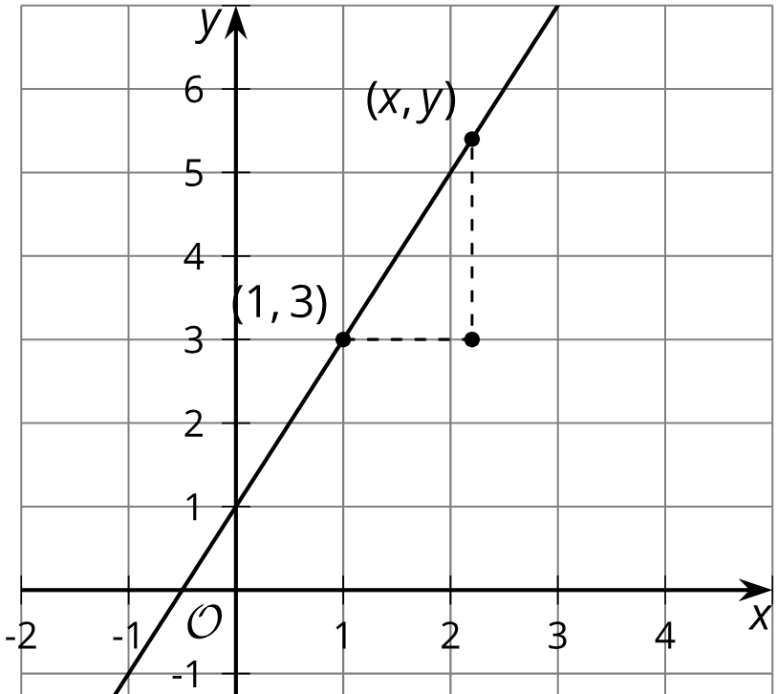
1. The image shows a line. a. Write an equation that says the slope between the points (1, 3) and (x, y) is 2.
b. Look at this equation: y – 3 = 2(x - 1). How does it relate to the equation you wrote?
2. Here is an equation for another line: y – 7 = (x – 5). a. What point do you know this line passes through?
b. What is the slope of this line?
3. Next, let’s write a general equation that we can use for any line. Suppose we know a line passes through a particular point (h, k). a. Write an equation that says the slope between point (x, y) and (h, k) is m.
b. Look at this equation: y – k = m(x – h). How does it relate to the equation you wrote?
9.3: Using Point-Slope Form
1. Write an equation that describes each line. a. the line passing through point (-2, 8) with slope
b. the line passing through point (0, 7) with slope
c. the line passing through point (, 0) with slope -1
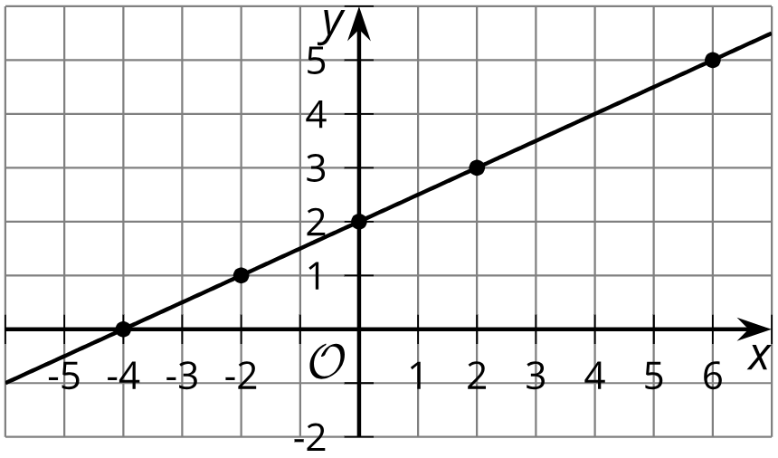
d. the line in the image above
2. Using the structure of the equation, what point do you know each line passes through? What’s the line’s slope? a. y - 5 = (x + 4)
b. y + 2 = 5x
c. y = -2(x - )
Lesson Synthesis: Equations of Lines
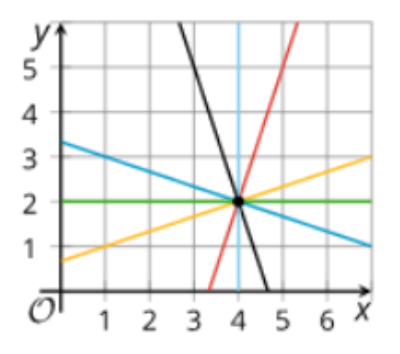
1. What do you notice?
2. Write the equations of at least 3 different lines shown.
Learning Intentions and Success Criteria
- Generalize (using words and other representations) that a line can be represented by an equation in point-slope form.
- Use the definition of slope to write the equation for a line in point-slope form.
Cool-Down: Same Slope, Different Point
Consider the line represented by: y + 4 = (x – 9) Write an equation representing a different line with the same slope that passes through the point (3, 6).
