Das Prinzip von Cavalieri
Bonaventura Cavalieri (1598 – 1647), ein Italiener, war einer der fähigsten Mathematiker seiner Zeit. Er war ein Schüler von Galileo Galilei, von dem Du vielleicht auch schon gehört hast. Schon mit 31 Jahren wurde er Professor für Mathematik an der Universität von Pisa. Cavalieri überlegte sich ein Prinzip, mit dem man den Flächeninhalt vieler Figuren und sogar den Rauminhalt (Volumen) vieler Körper leicht berechnen kann. Dieses Prinzip ist so wichtig und genial, dass es seinen Namen trägt: das Cavalieri'sche Prinzip. Jeder Mathematiker kennt es (und ab heute auch du!).
Aufgabe
Auf dem Tisch liegt ein Stapel Karten. Wenn Du sie sauber und ordentlich stapelst, dann sieht der Stapel von vorne ungefähr so aus wie rechts. Du kannst die Karten aber auch schief aufstapeln. Das sieht dann von vorne in etwa so aus wie links. Bewege die roten Punkte um den linken Stapel zu verändern.
Hat sich der Flächeninhalt der vorderen Fläche dadurch verändert? Offenbar hängt der Flächeninhalt nur von der Länge und der Höhe des Stapels ab, nicht aber von seiner Form. Das ist das Prinzip von Cavalieri!
Genauso kann man sich das z.B. an einem Dreieck überlegen, wenn man es sich in dünne Scheiben zerschnitten vorstellt:
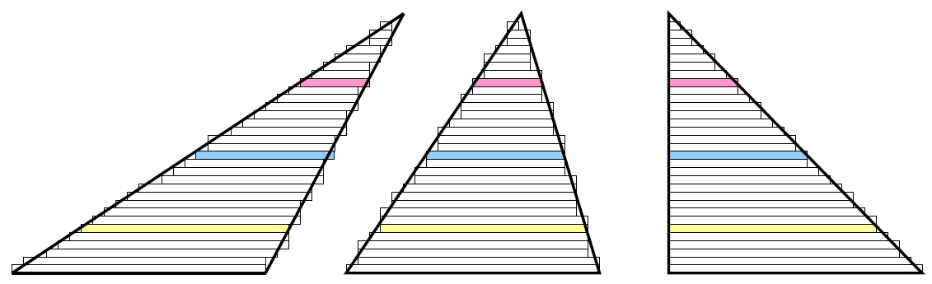
Scheiben in gleicher Höhe haben jeweils den gleichen Flächeninhalt, sie sind nur horizontal verschoben worden. Also müssen auch die 3 Dreiecksflächen gleich groß sein.
