OBERSUMME/UNTERSUMME -> INTEGRAL
Obersumme/Untersumme → Integral
Nun werden wir mit Hilfe von GeoGebra zeigen, wie sich die Unter-/Obersumme für große n dem Integral annähert.
- Tippen Sie den Befehl „Untersumme(f, 0, 4, n)“ in die Eingabezeile ein. Blenden Sie, der Übersichtlichkeit halber, die Funktion g(x) und alle unnötigen Punkte sowie die Tangente aus, so dass lediglich Funktion f zu sehen ist. (Klicken Sie dazu im Algebra-Fenster auf die blauen Punkte.)
- GeoGebra erstellt für n automatisch einen Schieberegler, dieser erscheint auf der Grafikansicht. Klicken Sie mit der rechten Maustaste auf den Schieberegler. Ganz unten finden Sie „Eigenschaften“. Öffnen Sie diese. Unser Schieberegler soll nur ganzzahlige, positive Werte annehmen. Nutzen Sie die folgenden Einstellungen:
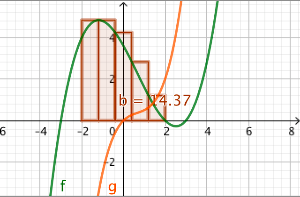
- Bewegen Sie nun den Punkt auf dem Schieberegler wird die Untersumme mit 1,2,...,25 Rechtecken angezeigt und berechnet. Diese Werte wollen wir nun graphisch darstellen.
- Unser Schieberegler heißt jetzt n und unsere Untersumme b. Klicken Sie auf die Untersumme dann wird der Name angezeigt. (Ist der Name nicht b, merken Sie sich einfach den Namen und passen die Befehle an.)
- Öffnen Sie nun die 2.Grafikansicht. (Menüleiste: Ansicht)
- Tippen Sie nun in die Eingabezeile „(n,b)“ ein. So entsteht in der Grafikansicht 2 ein Punkt mit den Koordinaten n (Anzahl der Rechtecke) und b (jeweilige Untersumme).(Sollte der Punkt in Grafikansicht 1 zu sehen sein, öffnen Sie die Eigenschaften (wie unter (2) beschrieben) und wählen Sie unter „Erweitert“ „Grafik2“ aus.
- Jetzt müssen nur noch die Einstellungen angepasst werden. (Mit Rechtsklick auf den Punkt können Sie die Spur anzeigen lassen.Wenn Sie in der Werkzeugleiste auf das Symbol klicken, können Sie die Achsen anpassen: Bewegen Sie dazu die Maus auf die Achsen und verlängern/verkürzen Sie die Achsen durch ziehen.)
- Bewegen Sie den Punkt über den Schieberegler.
- Stellen Sie zusätzlich die Obersumme graphisch dar.