Images. Placing points on a sphere such that the each point is the geometric median of all its other points.
By optimal placement we mean the placement of points on the sphere in such a way that each point is the geometric median of all its other points. The algorithm allows you to find only the placement with the values of highest Distance Sum. To find other symmetric arrangements of particles on a sphere it is possible (for example) as in https://www.geogebra.org/m/hw9hhq3h. As it turns out,
-for optimal placements, it is characteristic that the each point is not only a geometric median but also the geometric center of all its other points,
-for a given number of n points, the number of different such optimal placements on the sphere can be 0, 1, 2 , ... .
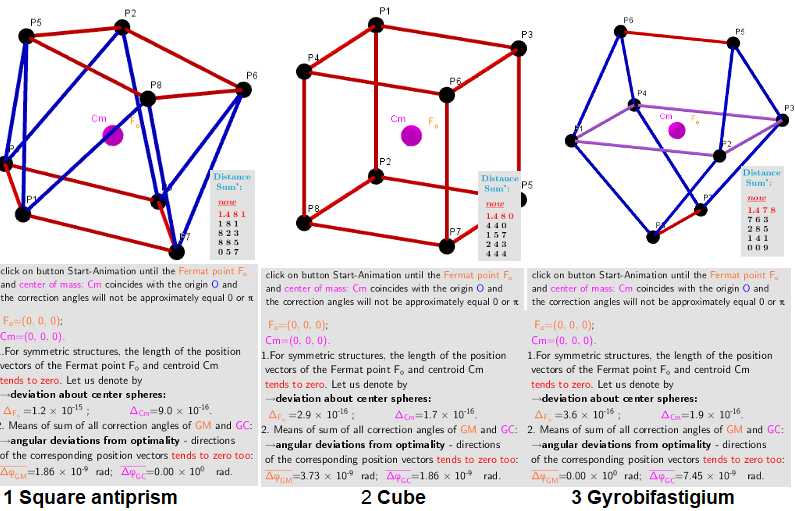
An example is the case of n=8: 1, 2, 3. The second solution corresponds to the case of uniform distribution of points on the sphere. For the cases n=12 and n=14 are found two optimal placements.
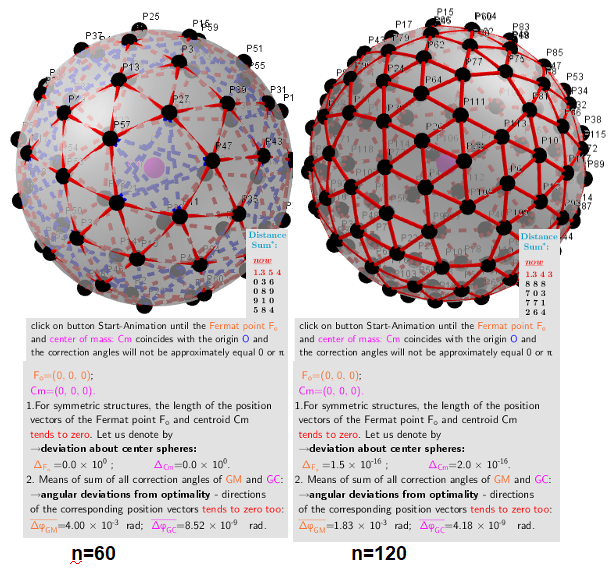
Examples n=60, 120 are close to a uniform distribution of points on the sphere and are not optimal!
n=8. Three different optimal arrangements of points on the sphere.
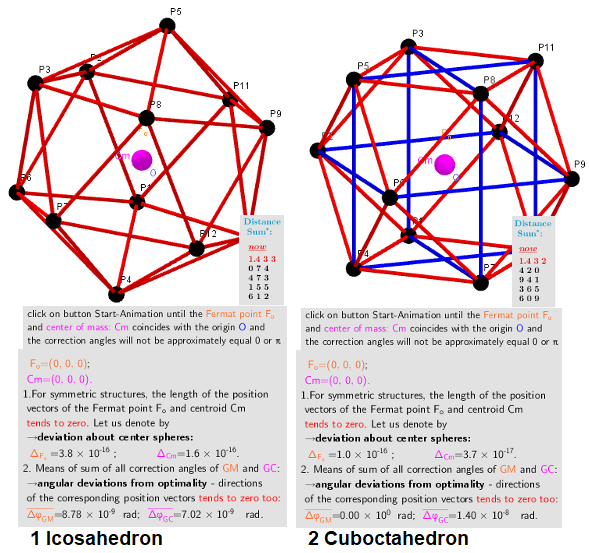
n=12. Two different optimal arrangements of points on the sphere.
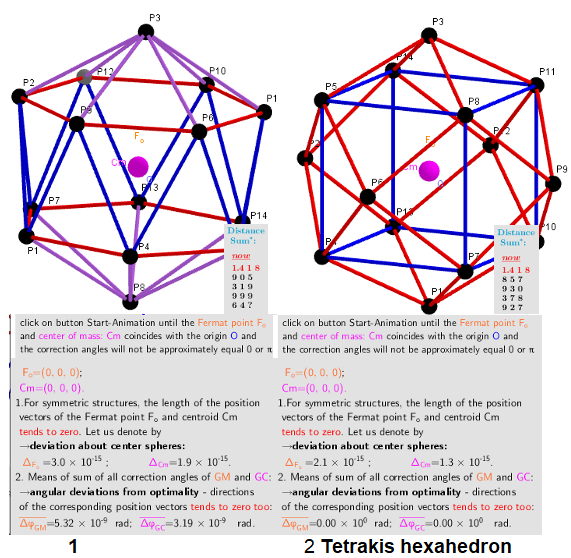
n=14. Two different optimal arrangements of points on the sphere.
Examples n=60, 120 close to a uniform distribution of points on the sphere are not optimal. Each point is not a geometric median and at the same time is the geometric center of all its other points.