La funzione inversa
Data una funzione , si definisce funzione inversa quella funzione che inverte l'input con l'output, cioè la con la : essa è permette quindi, a partire da un elemento di tipo , a trovare il corrispondente elemento di tipo che lo genera secondo la funzione originale.
Ad esempio se consideriamo la funzione , che ad ogni stato associa la corrispondente capitale , la sua inversa sarà , che ad ogni capitale associa uno stato .
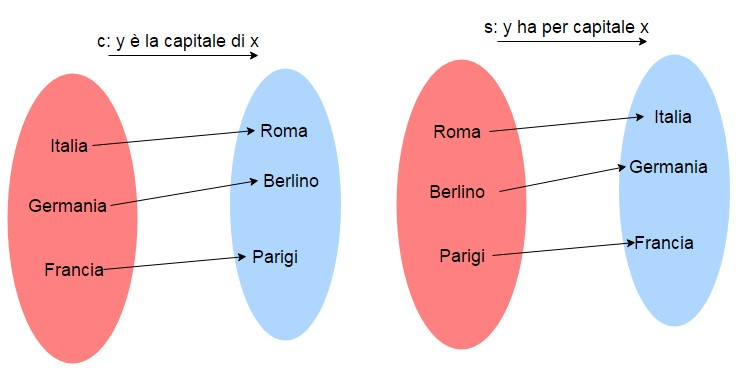
Vediamo che stati e capitali si scambiano il ruolo di ed , perchè per la funzione c gli stati sono la variabile indipendente (la ) e le capitali sono la variabile dipendente (la ), mentre per la funzione s vale il contrario.
Per indicare la funzione inversa si utilizza spesso una notazione pseudo-esponenziale, per cui l'inversa della funzione viene indicata con , similmente a come un'esponente negativo inverte una frazione.
Notiamo infine che se consideriamo l'inversa di una funzione inversa, riotteniamo la funzione di partenza. Possiamo dire insomma che .
INVERTIRE LE FUNZIONI MATEMATICHE: FUNZIONI ALGEBRICHE
Le funzioni inverse si definiscono ovviamente anche per le funzioni matematiche. Consideriamo il seguente esempio.
ESEMPIO 1
Giorgia lavora come rider e guadagna 2€ al giorno più 3€ per ogni consegna.
domanda 1a: scrivi l'espressione della funzione guadagno che ti permette di calcolare gli euro guadagnati da Giorgia in un dato giorno sapendo il numero di consegne effettuate in quel giorno. Rappresentala poi sul piano cartesiano.
Si tratta di una funzione è piuttosto semplice, la cui espressione è . Essendo descritta da un'espressione di primo grado, il suo grafico è una retta, come mostrato qui sotto.
I guadagni di Giorgia in funzione del numero di consegne
Per Giorgia però forse è più interessante (ma non meno deprimente) un'altra funzione: quella che le dice, data una quantità di soldi che vuole guadagnare quel giorno (ad esempio per pagarsi la cena), quante consegne deve effettuare per ottenere quel guadagno.
Domanda 1b: Trova l'espressione della funzione che dato la quantità di euro che Giorgia vuole guadagnare, permette di calcolare il numero di consegne che deve effettuare per ottenere tale guadagno.
Domanda 1c: rappresentala sul piano.
Puoi vedere che questa è la funzione inversa di quella precedente, in fatti la prima funzione aveva come dato di partenza il numero di consegne ed attraverso di questo calcolava il guadagno finale
![Per la funzione [math]g[/math] l'[i]input[/i] (variabile indipendente) è costituito dal numero di consegne, mentre il guadagno finale è il risultato ([i]output[/i] o variabile dipendente).](https://beta.geogebra.org/resource/mup4dgqp/K2XFuUKNovI7TIIU/material-mup4dgqp.png)
La nuova funzione che stiamo cercando, invece, considera come input il guadagno da ottenere, mentre il risultato del calcolo sarà il numero di consegne da fare. Abbiamo quindi scambiato il ruolo delle due grandezze, e la scrittura indica appunto che si tratta della funzione inversa di quella precedente.
![Per la funzione [math]g^{-1}[/math] l'[i]input[/i] (variabile indipendente) è il guadagno da ottenere, mentre il numero di consegne diventa il risultato ([i]output[/i] o variabile dipendente).](https://beta.geogebra.org/resource/sgu9z5jx/piEY8Ftm1hroQy77/material-sgu9z5jx.png)
ATTENZIONE: quando rappresentiamo le funzioni sul piano cartesiano, l'input (o variabile indipendente) viene posta sull'asse delle mentre l'output (il risultato, o variabile dipendente) si legge su quello delle . Di conseguenza quando si rappresenta una funzione e la sua inversa, le grandezze rappresentate su ognuno dei due assi vengono scambiate, dato che ad esempio nel nostro esempio le rappresenteranno le consegne per la funzione e gli euro per .
Questo è particolarmente evidente se diamo un'unica rappresentazione "circolare" che includa sia la funzione che la sua inversa; in questo caso non è possibile utilizzare le etichette ed , dato che non si tratta di attributi "assoluti" ma cambiano appunto a seconda della "direzione" che vogliamo percorrere per unire le due grandezze: quello che è la per é la per , e viceversa.
![Quello che per la funzione [math]g[/math] è l'[i]input[/i], per la sua inversa [math]g^{-1}[/math] è l'[i]output[/i], e viceversa.](https://beta.geogebra.org/resource/jy78htt2/qzC06Cwqn2gfFuDz/material-jy78htt2.png)
Vediamo come calcolare l'espressione della funzione inversa che ci permetta di effettuare il calcolo richiesto. Notiamo cheper ottenere la funzione inversa basta invertire la formula descritta dalla funzione, utilizzando come al solito i principi di equivalenza.
Partendo dalla funzione originale, che nel nostro caso è , invertiamo la formula con i seguenti passaggi:
cioè
.
Vediamo ora l'interessante relazione che c'è tra il grafico di una funzione e quello della sua inversa. Poiché le due relazioni si scambiano e , se la curva di passa per il punto possiamo essere sicuri che la curva di passa per . Facciamo un esempio con dei numeri.
Il guadagno di Giorgia quando fa zero consegne è ovviamente , ed è rappresentato sul piano dal punto .
Se vediamo la stessa situazione dal punto di vista della funzione inversa avremo che , cioè per guadagnare due euro Giorgia deve effettuare zero consegne. Ovviamente questo viene confermato dall'espressione algebrica della funzione inversa: , ed è rappresentato dal punto del grafico di .
Vediamo questo concetto rappresentato graficamente nella seguente animazione.
Di fatto nel grafico di una funzione e quello della sua inversa, le coordinate e si scambiano di posto - ovviamente la relazione è reciproca, dato che come abbiamo detto la funzione originale è a sua volta l'inversa della funzione inversa.
Questo porta ad una simmetria tra i due grafici che in generale vale tra qualsiasi coppia di funzioni che sono una l'inverso dell'altra: un grafico si può ottenere dall'altro "specchiandolo" rispetto alla retta bisettrice del I e III quadrante - che ha equazione ed il cui grafico che scambiando le coordinate si specchia in se stesso.
Vediamo meglio questa proprietà ripetendo l'analisi appena vista ma rappresentando le due funzioni sullo stesso piano. Dato che per ognuna di esse e rappresentano grandezze diverse, dobbiamo rinunciare ad attribuire alle due variabili un significato concreto e considerare le due funzioni come pure relazioni matematiche: e .
INVERTIRE LE FUNZIONI MATEMATICHE: FUNZIONI TRASCENDENTI
Il metodo dell'inversione della formula è perfetto per le funzioni algebriche, cioè quelle in cui alla variabile sono applicate le quattro operazioni (infatti i principi di equivalenza riguardano le quattro operazioni). Per le funzioni trascendenti, che applicano alla anche altri tipi di operazioni, trovare la funzione inversa è un'operazione che richiede un po' più di cautela e spesso è definita da una "nuova" funzione. Ad esempio, l'inversa dell'esponenziale è il logaritmo , per definizione stessa di logaritmo: proprio perché .
![Il logaritmo è definito come operazione inversa dell'esponenziale con la stessa base. Di conseguenza la [i]funzione[/i] logaritmo è l'inversa della [i]funzione[/i] esponenziale.](https://beta.geogebra.org/resource/qUVCGwQD/ixCEKGJxuQUwR7RK/material-qUVCGwQD.png)
Queste operazioni si possono combinare poi con le altre in un processo di inversione della formula simile a quello algebrico, ovviamente prestando attenzione alla precedenza delle operazioni, come al solito.
Se ad esempio vogliamo invertire la funzione procederemo innanzitutto come al solito invertendo la e , per sottolineare che vogliamo scambiare il "punto di partenza" e quello "di arrivo": . Procediamo poi eliminando le operazioni più "esterne", che in questo caso sono algebriche:
A questo punto abbiamo ottenuto ; la prossima operazione da cui "liberare" la è quella di logaritmo; per fare questo applichiamo l'operazione inversa, un esponenziale a base 5, ad entrambi i membri , esattamente come quando c'è una somma sottraiamo, o quando c'è una divisione moltiplichiamo.
Un altro modo per vedere questo passaggio è considerare che stiamo applicando la definizione di logaritmo.
e finalmente concludiamo sommando ad entrambi i membri e otteniamo: ; la funzione inversa è quindi .