Diagonalmatrix und Eigenvektoren Rn
Jordan-Normalform
Version für "beliebige" n - vorbelegt X=x1,x2....x9.
(Grundlagen und Beispiel Diagonalisieren - Jordan-Normalform)
Die Kriterien zur Diagonalisierbarkeit sind
- Das charakteristische Polynom zerfällt in Linearfaktoren
- Die Dimensionen der Eigenräume entsprechen den algebraischen Vielfachheiten der Eigenwerte
wobei mehrfache Eigenwerte entsprechend ihrer algebraischen Vielfachheit gezählt werden. Die Zusammenhänge könne unter anderem zur Kontrolle bei Eigenwertberechnungen verwendet werden. Im Applet wird nur der Fall algebraische Vielfachheit = geometrische Vielfachheit behandelt. Die Suche nach einem Hauptvektor im anderen Fall kann mit ergänzenden Schritten umgesetzt werden. Im PDF-Artikel (ggb im PDF-Anhang) sind einige Beispiele dokumentiert. Ich hab nicht versucht die Suche nach dem Hauptvektor zu automatisieren - es sind Eingriffe von Hand notwendig - es sieht auch nicht danach aus, dass dieser Schritt in GGB (alle möglichen Fallunterscheidungen) umgesetzt werden könnte. (4)(5)(6)(7) Charakteristisches Polynom Det| A-λE | = 0 Falls die Online Version eine undefinierte Variable E findet ===> Zeile (4) neu berechnen (7) Eigenwerte:= Eine Liste λi der Eigenwerte (8) DimEigenraum:= Eine Liste n-MatrixRang (A-λiE) = Dimension des Eigenraumes zu λi (Anzahl der Eigenvektoren) (10) Die Matrixgleichungen (A-λiE)=0 (12) LGλi Lineare Gleichungssysteme zu (8) λi zeilenweise (13) Aλi Löse LGλi zeilenweise (14) Matrixgleichungen Zeilenstufenform (16) Stelle fest welche freien Variablen zur Anwendung kommen (18) Eigenvektoren in Spalten mit unbestimmten Variablen der LGS LGλi (20) Eigenvektoren EVi entsprechend der Reihenfolge der Eigenwerte λi zeilenweise (21) Zusammensetzen der EV zur Matrix T (22) Bestätigung der Diagonalisierung T-1 A T = diag( λi ) (23) ggb-Command: JordanDiagonalization(A) (24..29) ggb-Commanda: CharacteristicPolynomial, MinimalPolynomial (27) Minimalpolynom: Stelle händisch Faktoren (A-λi E) zusammen deren Produkt die Nullmatrix ergeben (31) CharacteristicPolynom im Fall n=2DiagonalisierenMitEigenvektorenRn
Beispiel zur Anwendung
Beispiele
A:={{1, 1, 0 , 0},{1 , 1 ,-2 , 0 },{0 , 0 , 1 , -3 },{0, 0 , 0 , 7}}
A:={{0, 0, 0, 3}, {1, 1, 0,-1}, {0, 0, 2, 0},{1, -1, 0, 1}}
A:={{5, 0, 1 , -1},{0 , -3 , 0 ,0 },{0 , 0 , 4 , -4 },{ 1, 1 , 1 , 0}}
A:={{0, 0, 0 , 1},{1 , 0 ,0 , 0 },{0 , 1 , 0 , 0 },{ 0, 0 , 1 , 0}}
A:={{1, 1, 0 , 0},{1 , 1 ,-2 , 0 },{0 , 0 , 1 , -3 },{0, 0 , 0 , 7}}
A:={{2, -3, 1}, {3, 1, 3},{-5, 2, -4}}
A:={{-2, 5, 3}, {0, 2, 0}, {-4, 5, 5}}
A:={{0, -2, 1}, {2, -1, -1}, {-2, -2, 3}}
A:={{-1, 3, -2}, {2, 6, -5}, {2, 8, -7}}
A:={{0, 2},{2 , 3 }}
A:={{3, 2},{2 , 6}}
Elementarmatrizen:
Zeilen/Spalten-Operationen
Ex(zle,spl,k_f):=Sequence(Sequence(Element(Identity(n), zz,ss)-1*(zle==spl && zle==zz && spl==ss)*1+If(zz==zle && ss==spl,k_f,0),ss,1,n),zz,1,n); Ex(a,b,c) A: Addiere c*Zeile b zu Zeile a (Zeile a + c*Zeile b) ===> Multiplikation von Links
A Ex(a,b,c): Addiere c*Spalte a zu Spalte b ===> Multiplikation von Rechts
Zeilen/Spaltentausch
Tx(zz,ss):=Sequence(Element(Identity(n), If(kk≠zz ∧ kk≠ss,kk,If(kk=zz,Max(zz,ss),Min(zz,ss)))),kk,1,n);
Ex(a,b,c) A: Addiere c*Zeile b zu Zeile a (Zeile a + c*Zeile b) ===> Multiplikation von Links
A Ex(a,b,c): Addiere c*Spalte a zu Spalte b ===> Multiplikation von Rechts
Zeilen/Spaltentausch
Tx(zz,ss):=Sequence(Element(Identity(n), If(kk≠zz ∧ kk≠ss,kk,If(kk=zz,Max(zz,ss),Min(zz,ss)))),kk,1,n); 
 Ex(a,b,c) A: Addiere c*Zeile b zu Zeile a (Zeile a + c*Zeile b) ===> Multiplikation von Links
A Ex(a,b,c): Addiere c*Spalte a zu Spalte b ===> Multiplikation von Rechts
Zeilen/Spaltentausch
Tx(zz,ss):=Sequence(Element(Identity(n), If(kk≠zz ∧ kk≠ss,kk,If(kk=zz,Max(zz,ss),Min(zz,ss)))),kk,1,n);
Ex(a,b,c) A: Addiere c*Zeile b zu Zeile a (Zeile a + c*Zeile b) ===> Multiplikation von Links
A Ex(a,b,c): Addiere c*Spalte a zu Spalte b ===> Multiplikation von Rechts
Zeilen/Spaltentausch
Tx(zz,ss):=Sequence(Element(Identity(n), If(kk≠zz ∧ kk≠ss,kk,If(kk=zz,Max(zz,ss),Min(zz,ss)))),kk,1,n); 
Hauptvektorsuche
Ergänzungen zur Hauptvektorsuche (Add Cells)
(16) HVi=2;
der auf Hauptvektoren zu untersuchende EW(HVi)
(17) N:=3;
Potenz (A- λ E)^N um für den Eigenraum genügend Kandidaten (21), entsprechend alg. Vielfachheit von λ, zu erzeugen
(19) LGHV1:=(A - EW(HVi) E)^N
(20) LHV1:=Solutions(LGHV1 X,X)
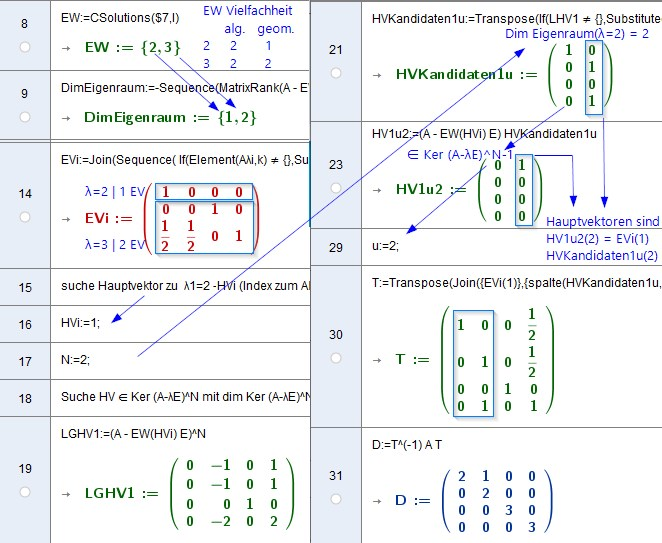
(21) HVKandidaten1u:=Transpose(If(LHV1 ≠ {},Substitute(Sequence(If(Element(LHV1,1,j) == Element(X,j),Flatten(Substitute(LHV1,Element(X,j) = 1)),0),j,1,n) \ {0},X = X0),{}))
Auswertung der Lösung LHV1 mit Darstellung der HV in Spalten der Matrix
(22) KernHV1:=(A - EW(HVi) E)^(N - 1) HVKandidaten1u
N>2: Kandidaten 1. Stufe prüfen - HV dürfen keine {0} Vektorspalte in KernHV1 haben
(23) u:=4
Ausgewählte Spalte von HVKandidaten1u ==> HV-Folge (Jordanblock) über die ausgewählte Spalte u
(24) HV1u2:=(A - EW(HVi) E) HVKandidaten1u
(25) HV1u1:=(A - EW(HVi) E) HV1u2
u1=HV1u1(u), u2=HV1u2(u), u3=HVKandidaten1u(u) - die HVs müssen eine Basis ergeben
(26) T:= Transpose(Join(Take(EVi,1,2),{HV1u1(u),HV1u2(u),HVKandidaten1u(u)} ) )
Take EVs and Append HVs - in diesem Fall werden die ersten zwei EVs und die HVs aus Spalte 4 der ersten HV-Stufe ausgewählt
Hauptvektorsuche R4