goniometrische uitwerking
afstand tussen de zwaartepunten van aangrenzende zijvlakken
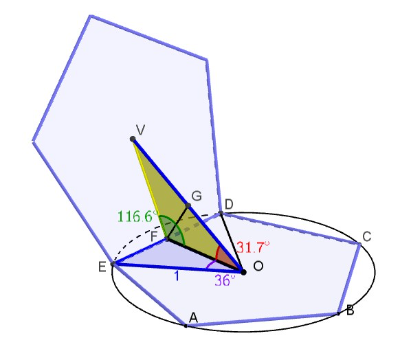
- Creëer binnen een cirkel met straal 1 een regelmatige vijfhoek.
- In deze vijfhoek is .
- De driehoek FOV is gelijkbenig met .
- Hieruit volgt
- De gezochte afstand tussen beide zwaartepunten O en V wordt dus .
afstand tussen de zwaartepunten van zijvlakken, door één zijvlak van elkaar gescheiden
- In het twaalfvlak is .
- De zwaartepunten O, V en W vormen een gelijkzijdige driehoek met waarin .
- In deze driehoek is
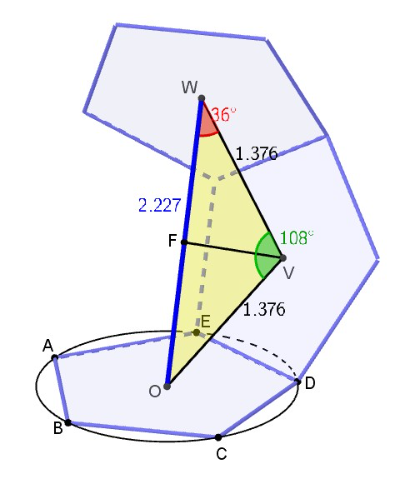
verhouding van beide afstanden
De hoek tussen [OV] en [VW] is gelijk aan 108°, zodat =36°.
Nu is de cosinus van 36° gelijk aan of .
Omdat kan je ook schrijven dat .
De fascinatie van de bewonderaars van de gulden snede dat je in een twaalfvlak drie gulden rechthoeken kunt tekenen die loodrecht op elkaar staan is m.a.w. te herleiden tot een eenvoudige meetkundige eigenschap:
- Bepaal eerst in een twaalfvlak de zwaartepunten van drie zijvlakken: twee aangrenzende zijvlakken een een derde zijvlak, aangrenzend aan het tweede zijvlak maar niet aan het eerste zijvlak.
- Construeer een hoek met hoekpunt het zwaartepunt van het eerste zijvlak en als benen de lijnstukken die het zwaartepunt van het eerste zijvlak verbinden met de zwaartepunten van het tweede en derde zijvlak.
- Vaststelling: de gevormde hoek in het zwaartepunt van het eerste zijvlak meet 36°.